Delta till Y och vice vera

Transformeringar

Syfte

Ibland kan ett komplicerat nät, som är svårt att räkna på, förenklas till ett enkelt nät genom delta till Y -transformering. Det nya nätet är sedan ofta enkelt att räkna på.

Delta till Y -transformering

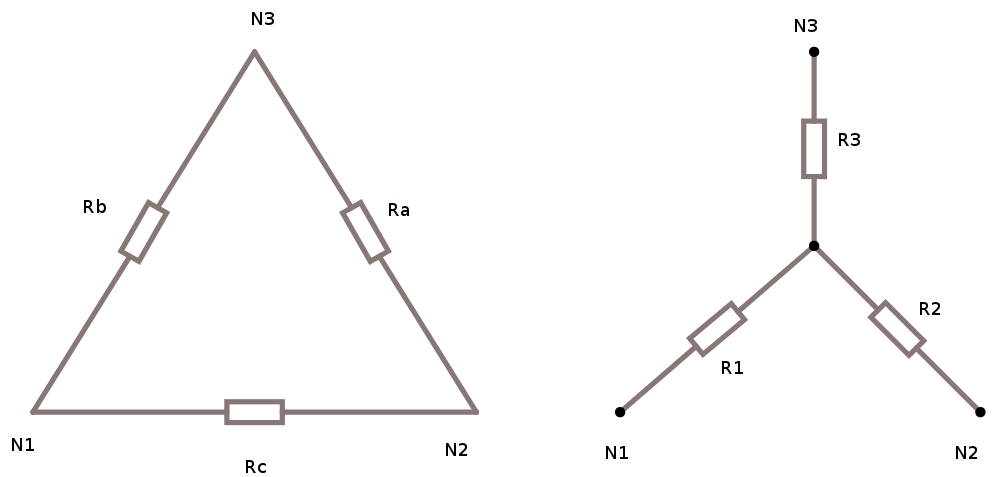
Räkna ut summan resistanserna och kalla det Rs.

Rs = Ra + Rb + Rc

Då är:

R1 = Rb * Rc / Rs
R2 = Rc * Ra / Rs
R3 = Rb * Ra / Rs

Försök se detta visuellt framför dig, hur det är uträknat. R1 ligger mellan Rb och Rc. R2 ligger mellan Rc och Ra. osv. Skissa upp detta på papper och återskapa formlerna visuellt så kommer det lossna rätt snabbt.

Y till delta-transformering

Räkna ut Rp = R1 * R2 + R2 * R3 + R1* R3

Då är:

Ra = Rp / R1
Rb = Rp / R2
Rc = Rp / R3

Även detta är enkelt om man tar det visuellt. Ra är på motsatt sida om R1. Rb på motsatt sida om R2. osv.

Exempel

Beräkna strömmen I. Om man studerar nedan krets en stund ser man snart att det finns en delta -koppling som går att konvertera till stjärnkoppling.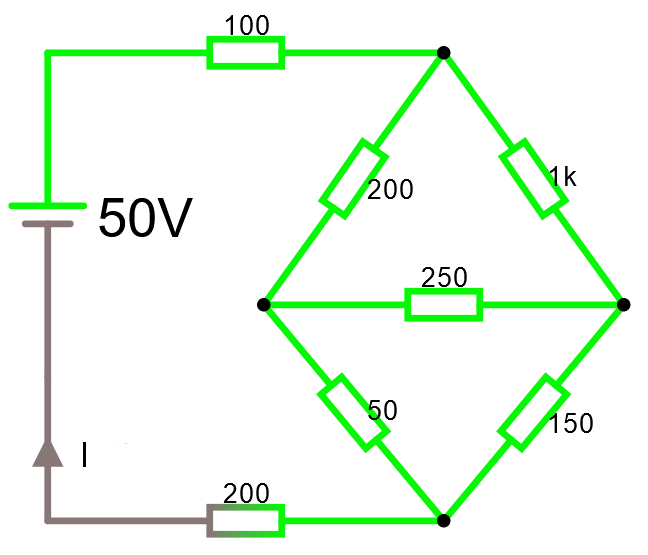


Om vi gör denna konvertering så får vi nedanstående krets istället. En löjligt mycket enklare krets, allt vi behöver göra är att räkna ut R1, R2 och R3.


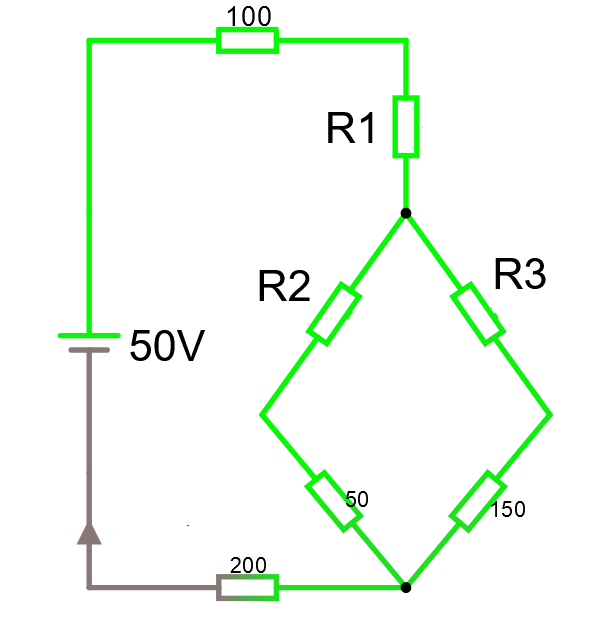
Vi konverterar från delta till Y. Vi börjar med att räkna ut summan av resistanserna inblandade. Rs = 1K + 250Ω + 200 Ω = 1.45K. Eller hur? Då är:

R1 = Rb * Rc / Rs = 1000*200 / 1450 = 137.93
R2 = Rc * Ra / Rs = 200 * 250 / 1450 = 34.48
R3 = Rb * Ra / Rs = 250 * 1000 / 1450 = 172.41

Dvs, vi kan nu förenkla ovan till

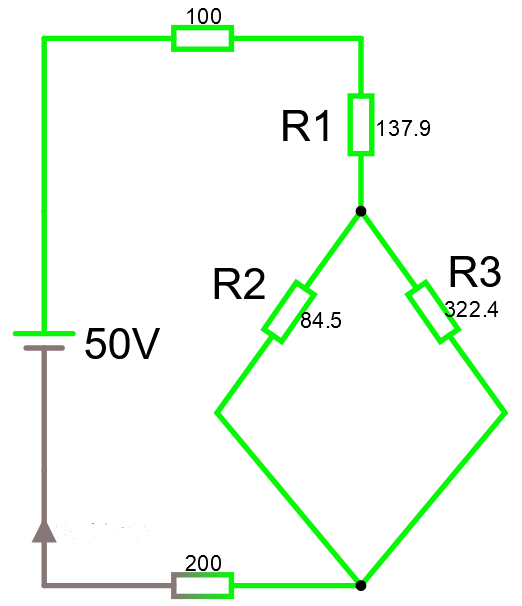
Som kan förenklas till

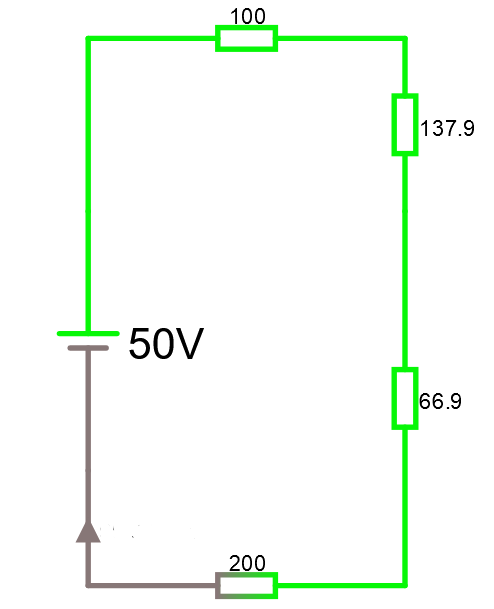
Som kan förenklas till



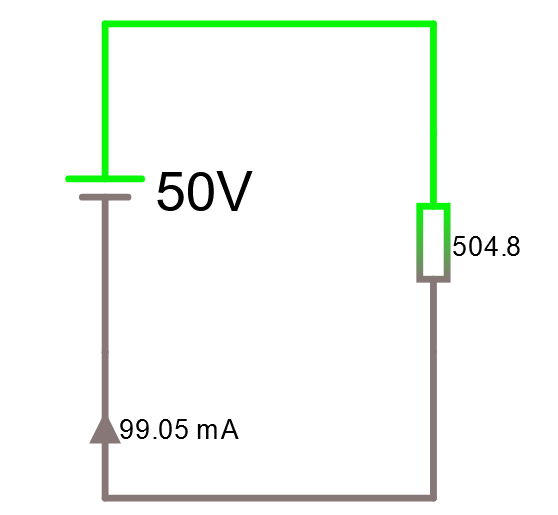
Studera kretsen i simulator före och efter transformeringen samt slutligen efter alla förenklingar av kretsen. Strömmen är densamma! (nästan, ackumulerande avrundningsfel gör att det skiljer någon tusendel)