Seriekoppling och parallellkoppling

Seriekoppling av resistanser

Seriekoppling är rätt så enkelt begripa. Om vi seriekopplar 3 motstånd på vardera 1KΩ så får vi en resistans på 3KΩ. Dvs, samma om vi seriekopplar 2 spänningskällor på vardera 6 volt, då får vi 12 volt.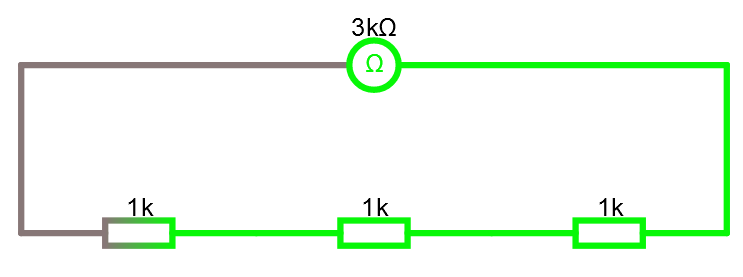



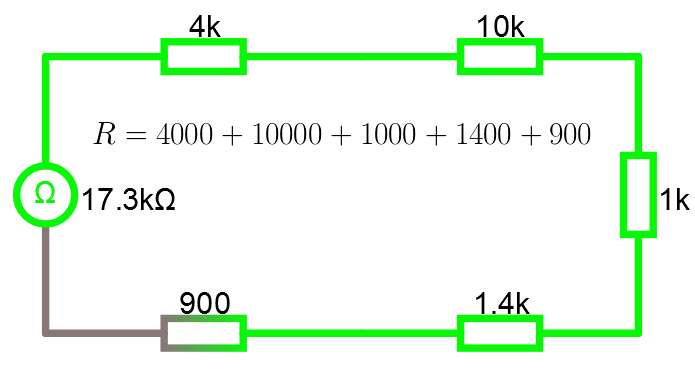
Öppna seriekopplingen i simulatorn.

Parallellkoppling av resistanser

Parallellkoppling är snäppet svårare matematiskt. Vi summerar här det inverterade värdet av resistanserna. Summan vi får inverterar vi och får då svaret. Dvs om vi parallellkopplar R1 och R2 och R3 så får vi: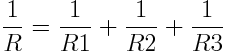





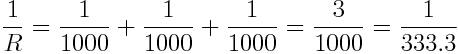
R = 333.3 Ω




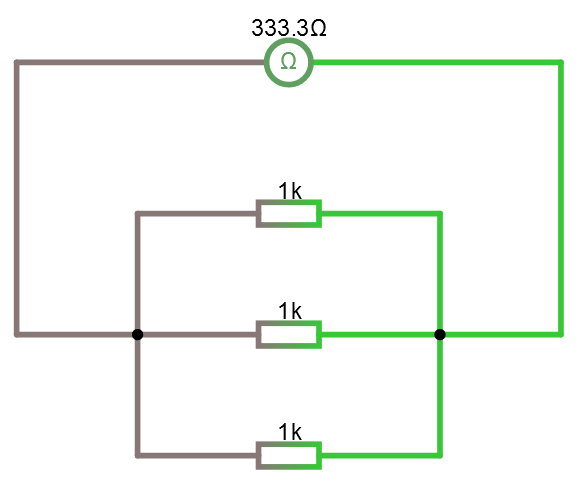
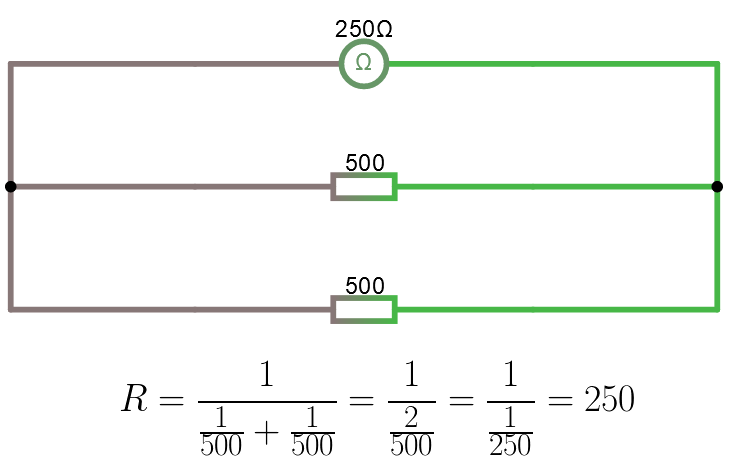
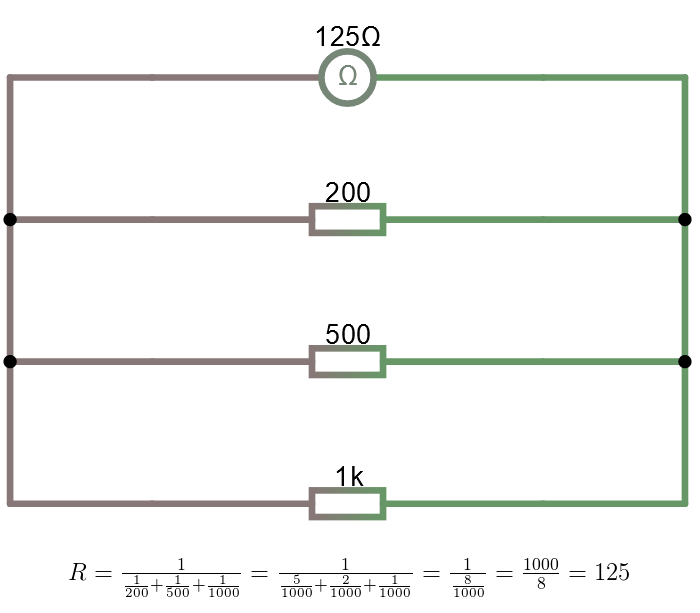
Öppna kretsen i simulatorn.

Serie + Parallellkoppling

Det går förstås att kombinera serie och parallellkoppling in absurdum. Det förekommer kanske inte så mycket i verkligheten men desto mer i skolböcker för att öva upp förmågan.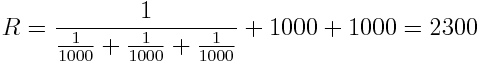




Kretsar som ser ganska avancerade ut går ibland att lösa enbart genom att successivt arbeta sig igenom vad som är seriekopplingar och parallellkopplingar. Studera följande exempel. Vad är resistansen mellan A och B ?


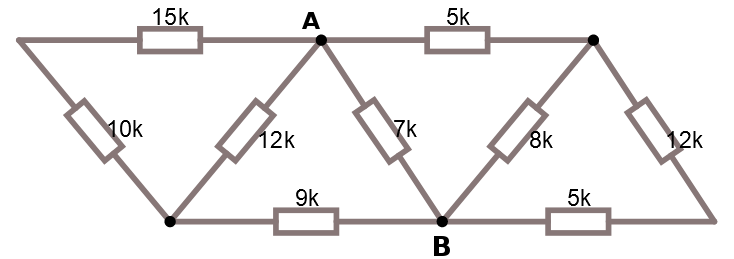
Vi ser genast att några seriekopplade resistanser går att slå samman.


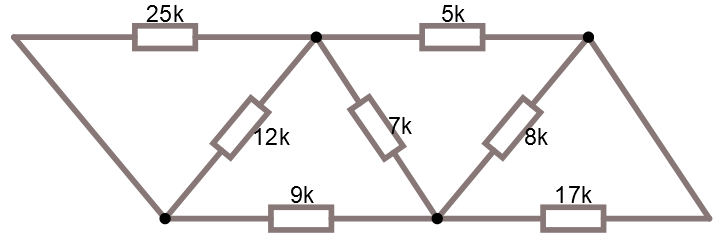
Sen ser vi att vi har några parallellkopplade som går att slå samman.


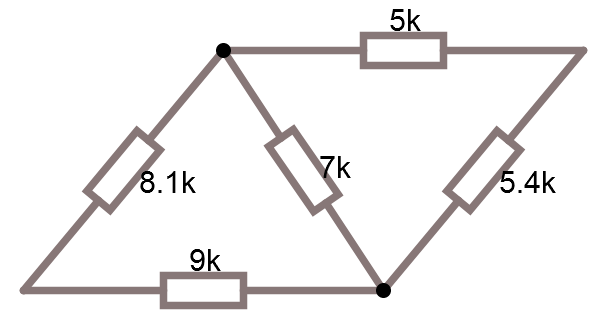
Sen har vi lite nya seriekopplade som går att slå samman.


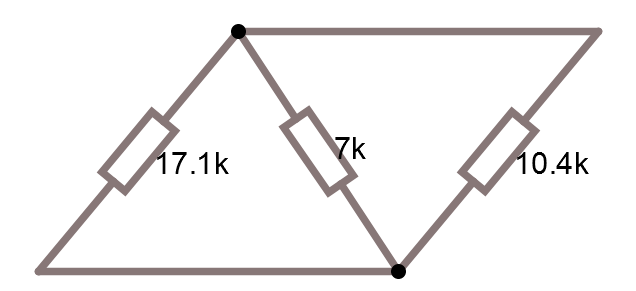
I slutändan har vi 3 stycken parallellkopplade resistanser som vi kan ersätta med en 3.4K -resistans mellan A och B vilket var det som efterfrågades.


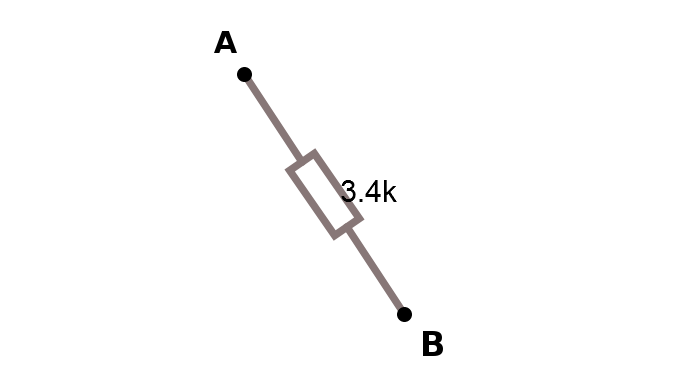
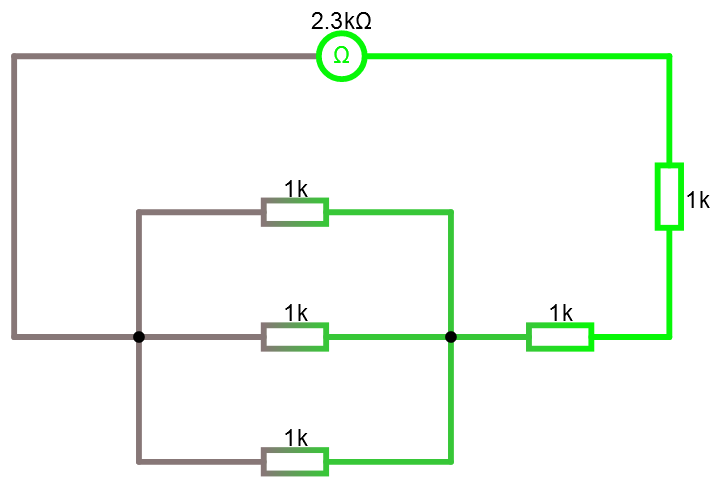
Här nedan ser du kretsen som den såg ut från början och kopplar vi in en resistansmätare i nätet ser vi att resistansen mycket riktigt var 3.4 KΩ.


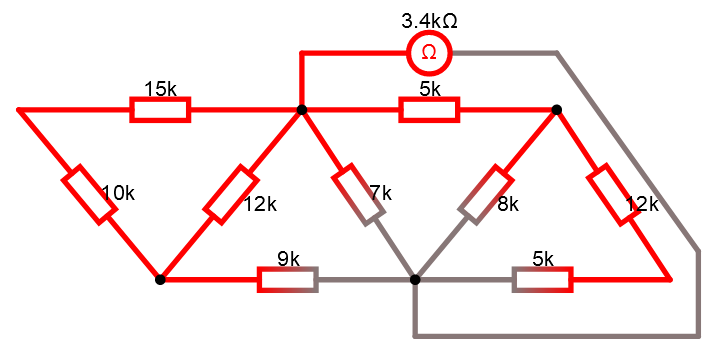
Studera kretsen i simulatorn.

Mer exempel

Vad är resistansen mellan A och B nedan? 3 stycken seriekopplade 220Ω resistanser blir 660Ω. Dessa 660Ω är sedan parallellkopplade med 220Ω.

1/R = 1/220 + 1/ 660. Rätt svar: 165Ω

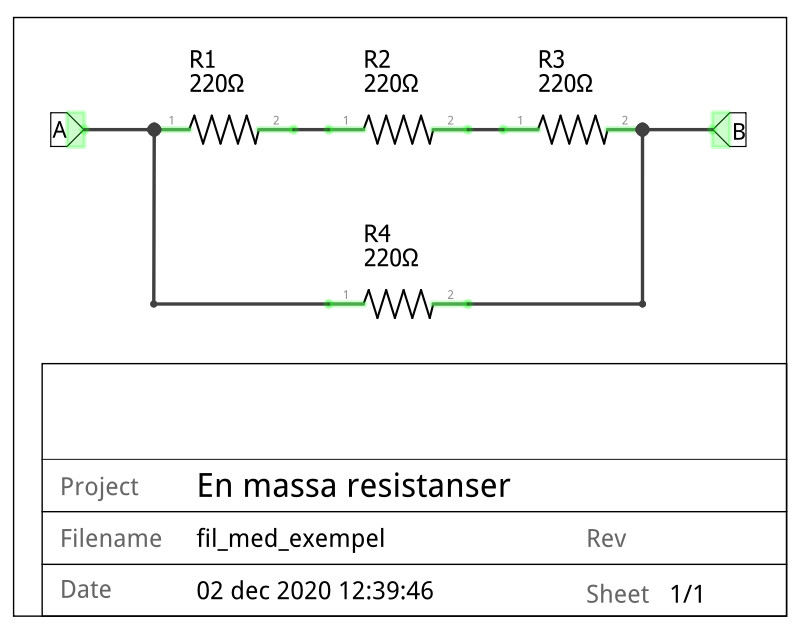
Resistanser på ett kretskort

Vad är resistansen mellan A och B nedan?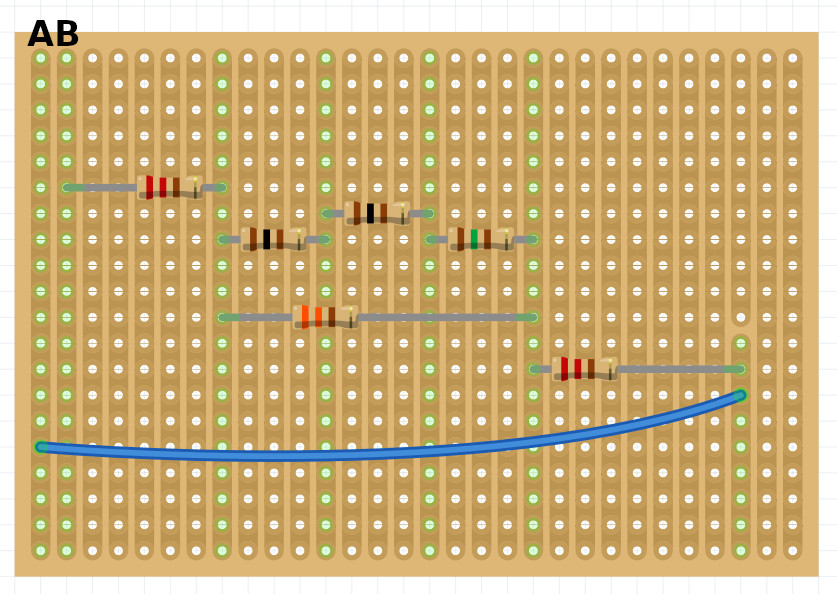




Uppkopplingen i elkretssimulatorn (titta inte innan du försökt själv!).

Färgkoden ger resistansen

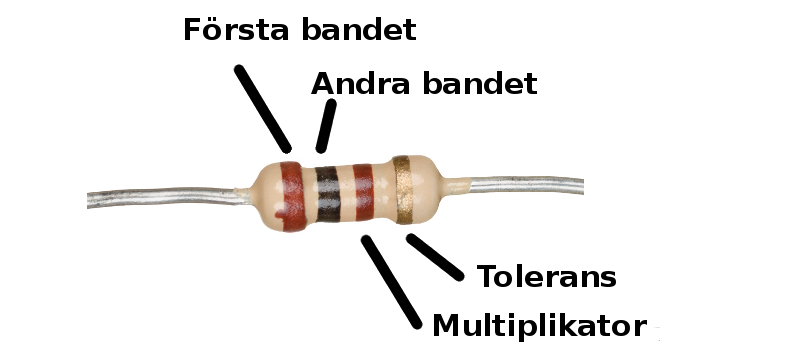
2 färgband

	1:a	2:a	3:e (multiplikator)	Tol.
Svart	0	0	x 1 Ω
Brun	1	1	x 10 Ω	1 %
Röd	2	2	x 100 Ω	2 %
Orange	3	3	x 1.000 Ω
Gul	4	4	x 10.000 Ω
Grön	5	5	x 100.000 Ω
Blå	6	6	x 1.000.000 Ω
Violett	7	7	x 10.000.000 Ω
Grå	8	8
Vit	9	9
Silver			x 0,01 Ω	10 %
Guld			x 0,1 Ω	5 %

Lite fusk:




Räkna ut resistans från färgkod.