Ohms lag
Lite repetition
Resistans mäts i Ohm (Ω)
Resistans mäts i Ohm som brukar skrivas med den grekiska symbolen Ω. Det finns ofta anledning att prata om väldigt stora resistanser och då använder man prefixen K (kilo, dvs tusen) och M (mega, dvs miljoner) framför Ω.2 KΩ = 2 000 Ω (tvåtusen ohm)
1 MΩ = 1 000 000 Ω (1 miljon ohm)
100 MΩ = 100 000 000 Ω (100 miljon ohm)
200 KΩ = 200 000 Ω (två hundratusen ohm)
Ström mäts i ampere (A)
Ström mäts i ampere och skrivs med symbolen A. Pratar vi om strömmar på flera ampere så är det oftast ganska höga strömmar. I kretsar är det annars vanligare med betydligt mindre strömmar, t.ex. tusendelar av en ampere och vi säger då milliampere (milli = tusendel).10 mA = 0.010 A (10 tusendelar av en ampere)
500 mA = 0.5 A (en halv ampere)
Spänning mäts i volt (V)
Som nämt tidigare mäts spänning i volt och här är det ganska vanligt att vi rör oss kring 0.5 volt och upp mot 50 volt i lågspänningssammanhang. Det vanligaste är kanske en spänning 1-12 volt. Pratar vi om KVolt (tusentals volt) så är det dödligt farliga spänningar. Spänningar i nivån millivolt (tusendelars volt) är så låga att det är hopplöst göra något vettigt.Symboler
Symbolen för spänning är U (mäts i volt med symbolen V), symbolen för ström är I (mäts i ampere med symbolen A) och resistans är R (mäts i ohm med symbolen Ω).Vi kan alltså säga att U = 5 V, vilket då betyder att spänningen är 5 volt. Eller att R = 1.2 KΩ vilket betyder att en resistans är 1.2 kilo ohm. Det är viktigt lära sig detta för att hantera nästa steg utan problem.
Ohms lag
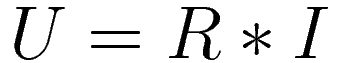
Lathund för ohms lag
Ohms lag säger vad som står här ovan. Om man vet resistansen och strömmen genom resistansen så kan man räkna ut spänningen över resistansen. Denna lag kan sedan skrivas om beroende på vilka 2 av de 3 storheterna man känner till.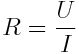
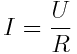
För att hålla reda på detta kan man tänka sig nedanstående magiska triangel som vi kan kalla "ohms lag", därför att det är ohms lag. Håll fingret över den symbol du vill veta så får du ekvationen. Vill du veta R eftersom du vet U och I, så håll fingret över R och du ser att där står U / I. Prova.
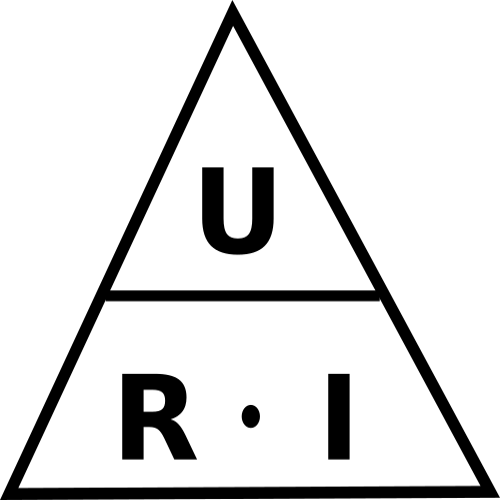
Exempel ohms lag
Med ovanstående symbol i minnet fixar du ohms lag lätt som en plätt. Studera nedanstående slutna krets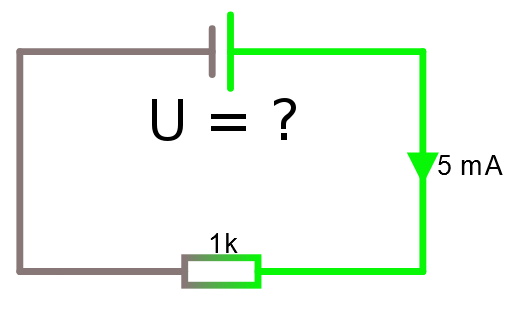
Om vi vet att resistansen är 1 KΩ och strömmen genom densamma är 5 mA. Vad är då spänningen över resistorn, vilket är samma sak som U? Med eller utan hjälp av ovan lathund vet vi att U = R * I = 1000 * 0.005 volt = 5 volt.
Vad är strömmen i nedanstående exempel?
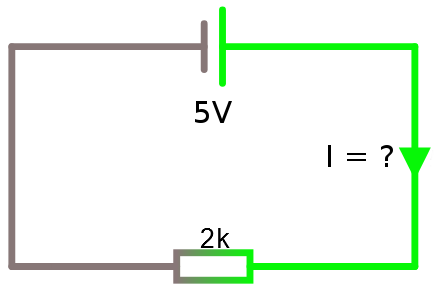
I = U / R = 5 / 2000 A = 0.0025 A = 2.5 mA
Vad är I1 och I2 nedan?
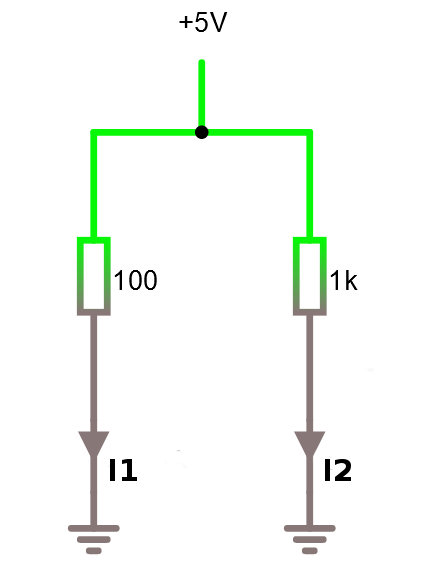
Svar: 50 mA resp. 5 mA.
Referensriktningar och polaritet
En inte så svår men mycket viktig grej att lära är att hålla reda på strömmens riktning och spänningens polaritet. Om man slarvar här kommer man trötta ut sig själv med alla knasiga fel som uppstår längre fram (matte, fysik & elektronik handlar egentligen bara om att vara noga och under resans väg undvika fel, resten är enkelt).Strömmen genom en resistor är riktad från högre potential (+) till lägre potential (-). Spänningen faller över resistorn.
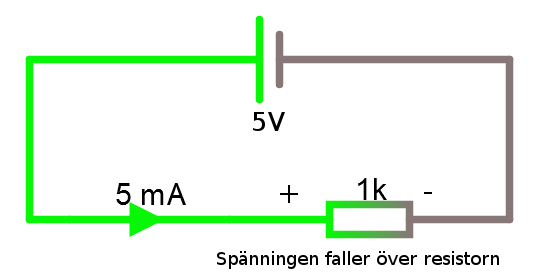
Räkna ut resistorn till en lysdiod
Säg att vi önskar IF = 20 mA = 0.02A genom lysdioden. Vidare vet vi att spänningsfallet är VF = 2 volt över lysdioden. Vår spänningskälla UKrets levererar 5 volt. Vad skall R vara?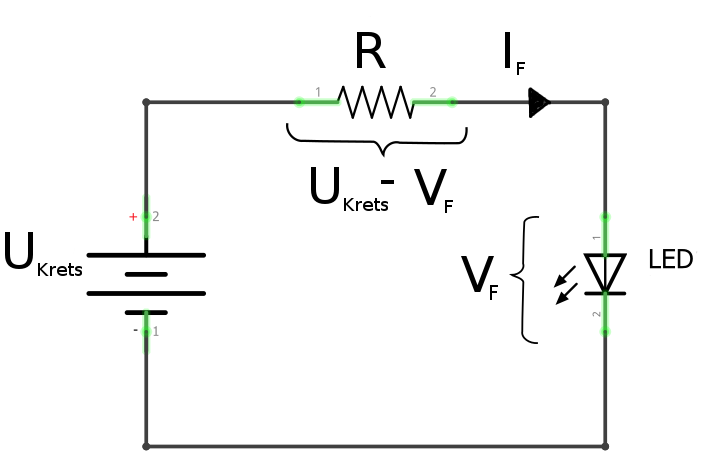
Svar: Vi vet att spänningen över resistorn är UKrets - VF = 5 - 2 volt = 3 volt. Ohms lag ger oss då att R = U / I = 3V / 0.02A = 150 Ω