2-poler

Thévenins teorem

Säg att du har en komplicerad krets.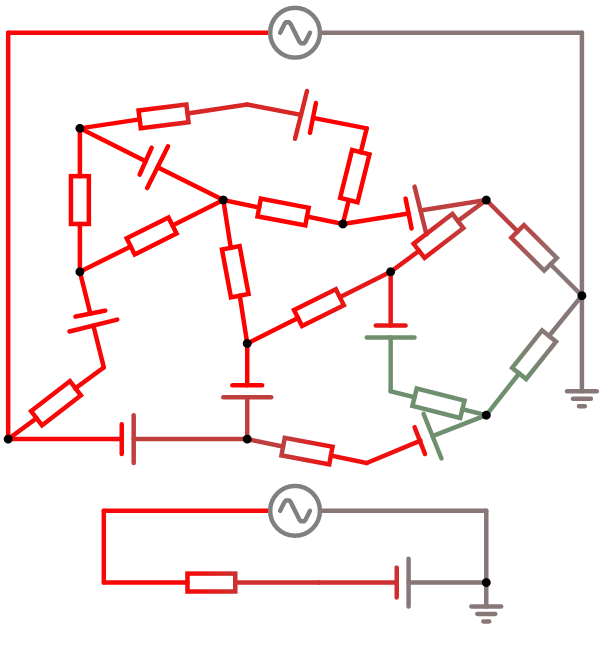


Under vissa förutsättningar kan denna troligtvis förenklas ganska mycket. Om det är en krets som består av spänningkällor och strömkällor och resistorer och den har 2 anslutningar ("2 poler") så kan den förenklas.

Thévenins teorem: En godtyckligt uppbyggd linjär tvåpol bestående av ström- och spänningskällor och resistorer, kan ersättas med en spänningskälla Vth och en resistor Rth i serie.

Detta gör vi genom att på kretsen ifråga:

1. Beräkna den ekvivalenta spänningen
2. Beräkna den ekvivalenta resistansen (vi kortsluter spänningskällan)

Studera nedan exempel.


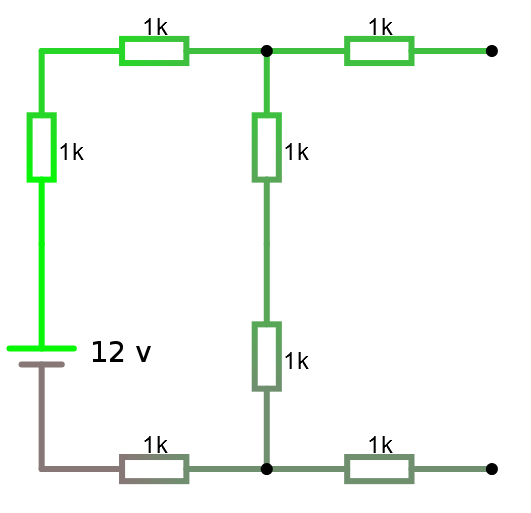
Vi börjar med att beräkna spänningen ut, dvs DB i figuren.



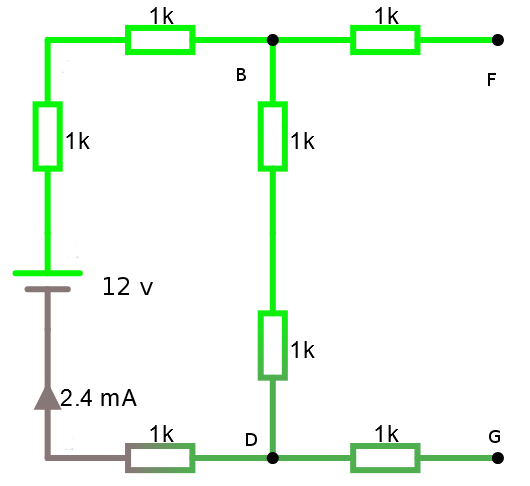
Strömmen i slingan är 2.4 mA och då borde spänningen DB ut bli U = 2.4 mA * 2KΩ = 4.8 volt. Eftersom utgången i 2-polen antas obelastad blir utspänningen också 4.8 volt.

För att räkna ut den ekvivalenta resistansen kortsluter vi vår spänningskälla och får följande schema.


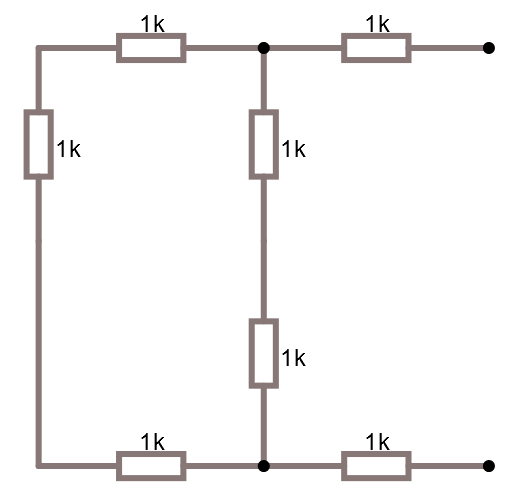
Vi kan förenkla detta till nedan och ser då att vi kan räkna ut resistansen lättare.


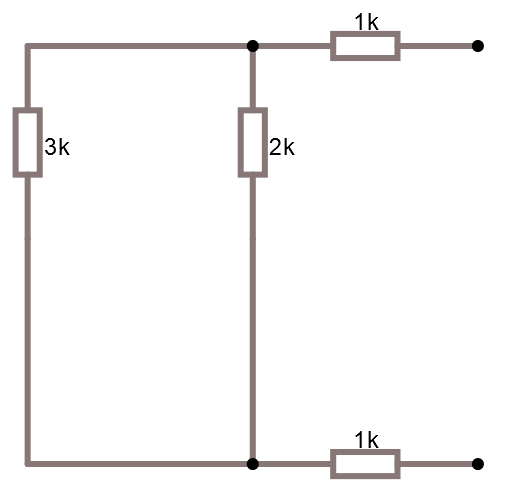
Om vi parallellkopplar 3K och 2K får vi



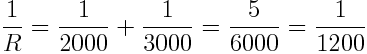
R = 1200

Utgående resistans är alltså 1.2 K + 1K + 1K = 3.2 K. Vi får alltså följande mycket enklare krets.



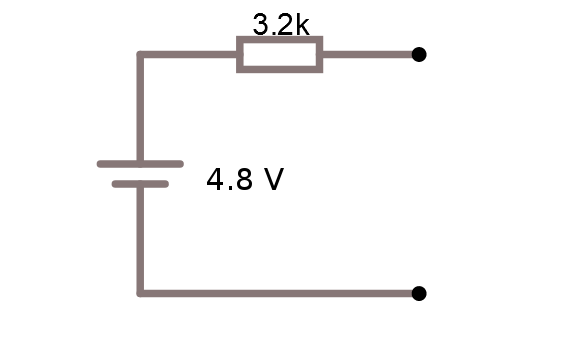
Stämmer detta? Låt oss titta på ursprungskretsen och koppla in någonting.


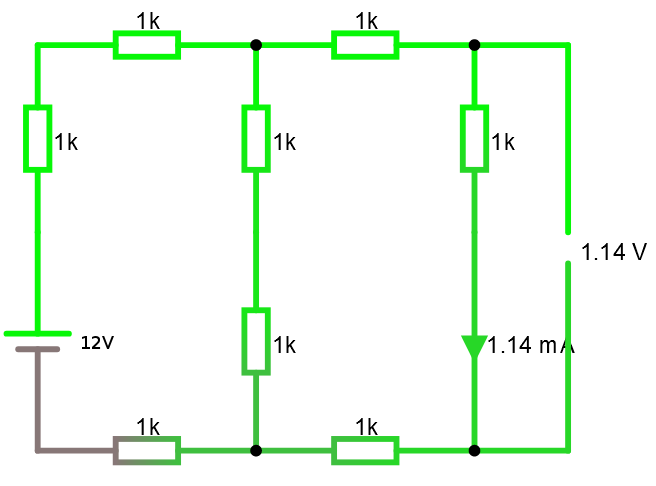
En liten last på 1 KΩ kopplas in och spänning däröver blir då (sjunker till) 1.14 volt.



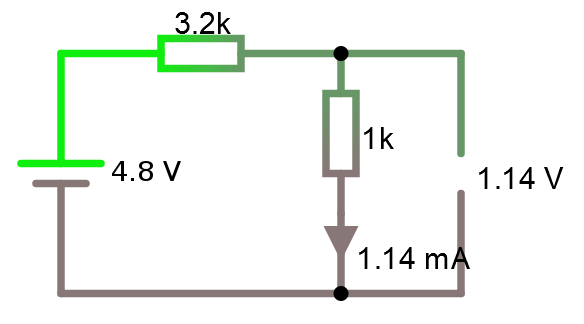
Jämför själv i simulatorn. Före och efter förenklingen av 2-polen.

Nortons teorem

Nortons teorem fungerar som Thévenins teorem fast med skillnaden att Thévenin ersatte tvåpolen med en spänningskälla och resistans i serie medans Nortons istället tänker sig en strömkälla parallell med en resistor.

Om man har en linjär tvåpol (elektrisk krets med två anslutningar) bestående av ström och spänningskällor och resistanser så kan denna ersättas med en ekvivalent krets bestående av en ideal strömkälla (nortonkälla), som genererar strömmen I, parallellkopplad med en resistor R.

Såhär går vi tillväga.

1. Beräkna strömmen (vi kortsluter utgången)
2. Beräkna den ekvivalenta resistansen (vi kortsluter spänningskällan)



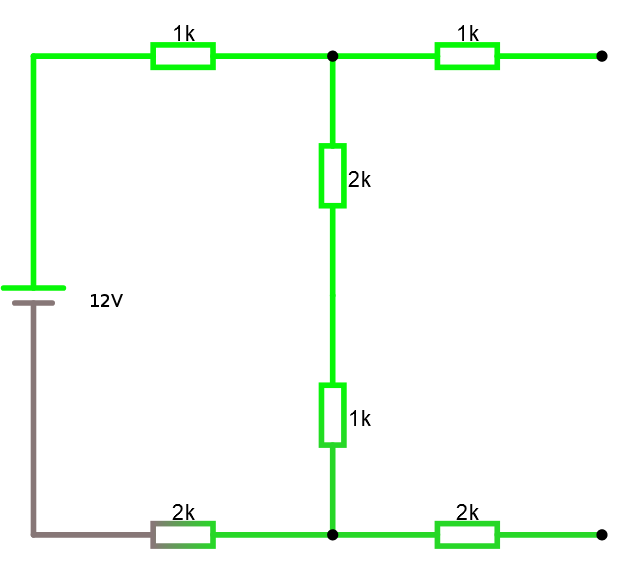
Vi kortsluter utgången och tänker oss en ström i denna kortslutning.


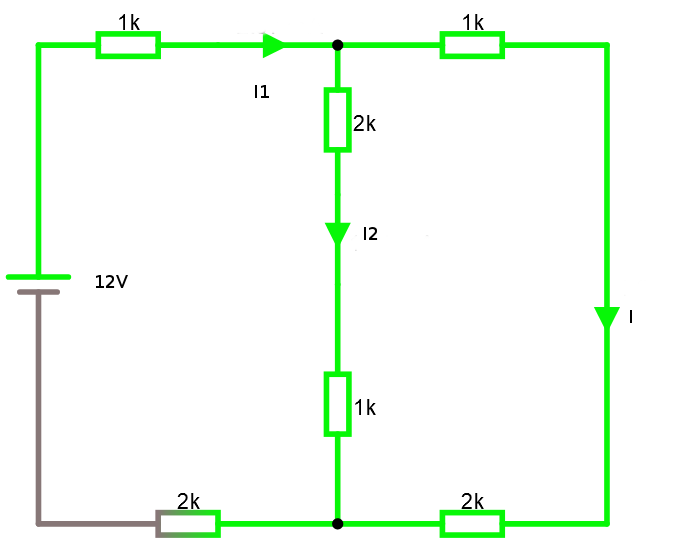
Vi kan slå ihop seriekopplingar så blir allt tydligare.

Parallellkopplade 3K -resistorerna motsvarar en resistans på 1.5 K. Det betyder att I1 = 12V / (3K+1.5K) KΩ = 2.66 mA. Nu ser man redan att I och I2 delar lika på denna ström. Men låt oss ändå räkna. Om strömmen är 2.66 mA då är spänningen över de parallellkopplade 3K -resistanserna U = R * I = 2.66 mA * 1500 Ω = 4 volt. Vi får sedan I = U / R = 4 V / 3000 Ω = 1.33 mA.


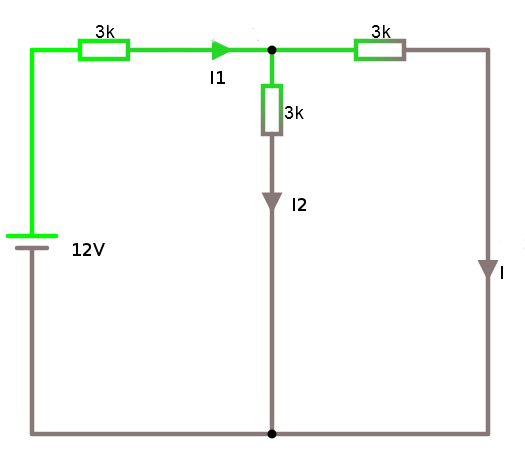
Titta på kretsen i simulatorn. Nästa steg är att räkna ut resistansen och då kortsluter vi spänningskällan.


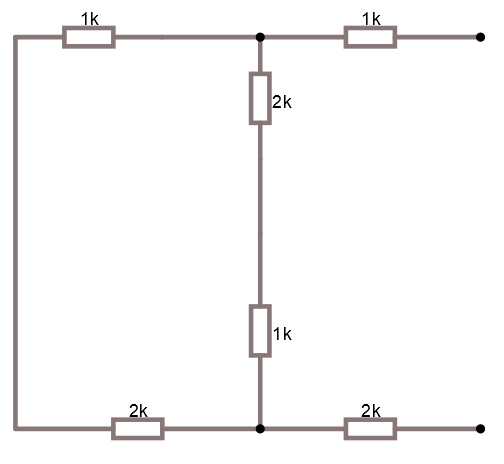
Här ser man då att resistansen är



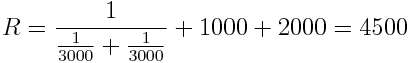
Dvs R = 4.5 KΩ



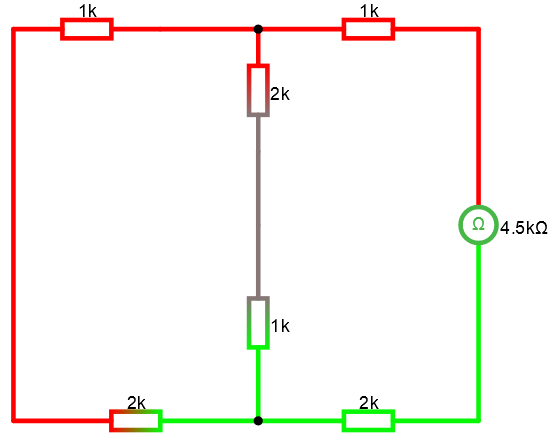
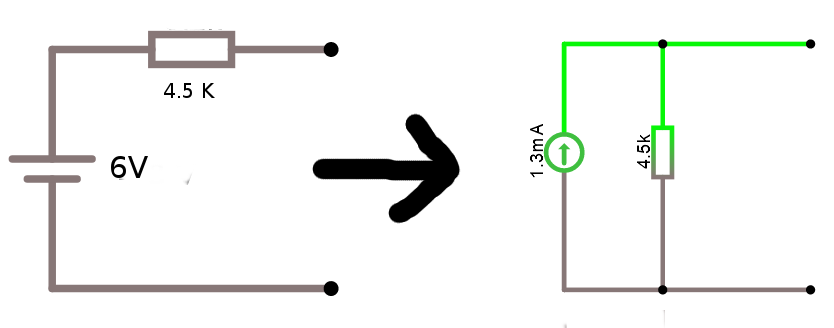
Vi har nu skapat vår norton -ekvivalent av 2-polen med strömgeneratorn 1.3 mA och R = 4.5 KΩ



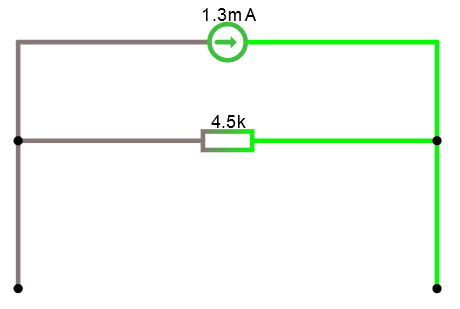
Okej, stämmer detta? Vi kopplar på en liten last och ser vad som händer.



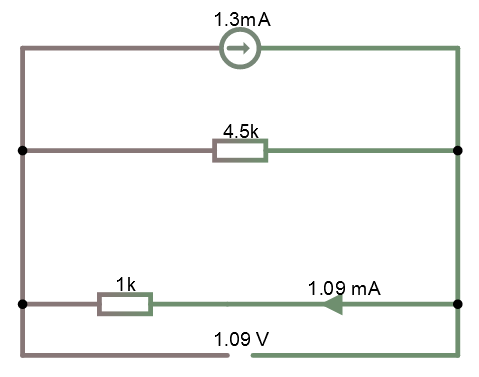
Titta på kretsen i simulatorn. Om vi går tillbaka till den ursprungliga kretsen och kopplar på samma last så ser det ut såhär.



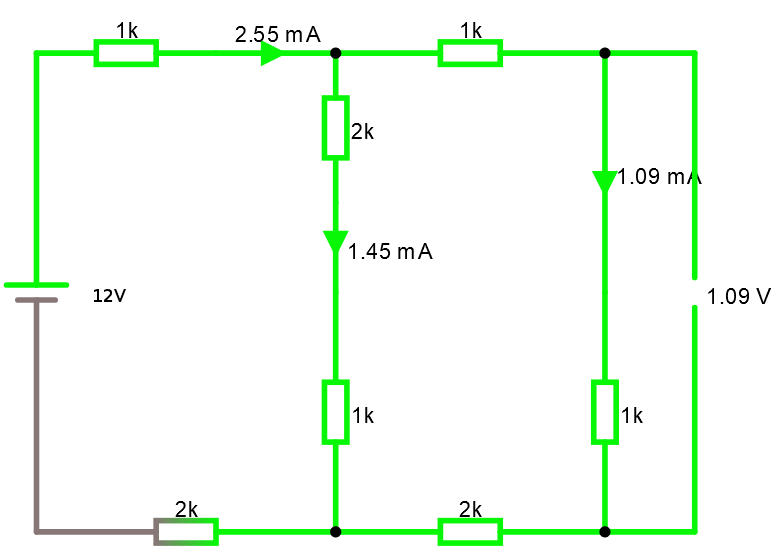
Titta på kretsen i simulatorn.

Omvandling mellan thevenin/norton

Det går att konvertera enkelt mellan Thevenin och Norton. Resistansen är alltid samma. Men strömkällan eller spänningskällan räknas om med hjälp av ohms lag .

I nedan exempel är resistansen samma men I = U / R = 6V / 4500 KΩ = 1.33 mA.