Kirchhoff
Räkna på strömmar
Kirchhoffs strömlag
Om man tänker sig en punkt i kretsen, så är alla strömmar in och ut ur denna punkt noll. Dvs, summan av alla ingående strömmar är lika stor som summan av alla utgående strömmar. Det är egentligen ganska enkelt, det enda vi behöver göra är att hålla reda på riktningen på strömmen och dess tecken. En utgående ström som är negativ är alltså egentligen en ingående ström.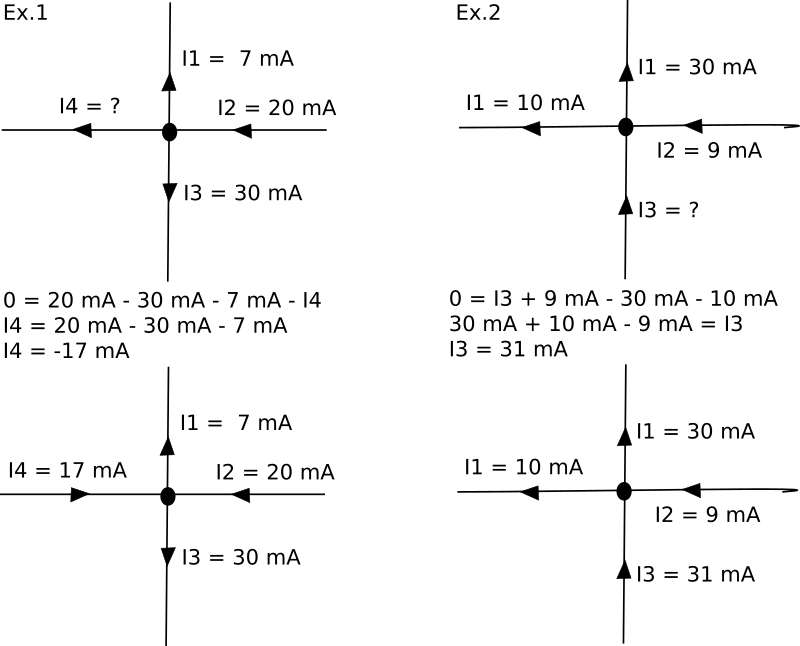
I ovan exempel summerar vi alla ingående strömmar i punkten med rätt tecken (en ingående ström som är negativ får alltså ett negativt tecken) och drar ifrån alla utgående strömmar i punkten även där med rät tecken (en utgående ström som är negativ får ett negativt tecken).
Svaret vi sedan erhåller kan vara positivt eller negativt. Vi kan då välja att antingen behålla riktningen på strömmen och dess tecken eller om tecknet är negativt så kan vi byta till ett positivt tecken och samtidigt ändra riktningen på strömmen. I exempel 1 ovan blev strömmen I4 = -17 mA. Nu tog jag bort tecknet här och bytte riktning. Observera att det är precis samma sak. Det är mer en skönhetsgrej hur man vill skriva. Det viktiga är att förstå hur det fungerar.
Exempel 1
Vad är strömmen I ?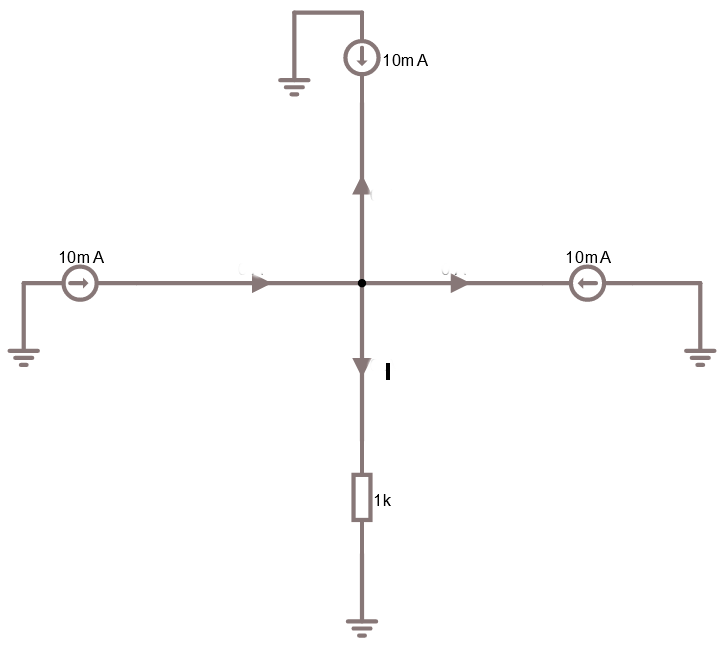
Summan av ingående och utgående strömmar är noll. Skissen är lite lurig. Vi kan ju titta på strömgeneratorerna så ser vi att
10 mA + 10mA + 10mA - I =0
I = 10 mA +10 mA +10 mA = 30 mA
Eller så kan vi ta fasta på riktningarna på strömmarna där 2 stycken då blir negativa.
10 mA - -10mA - -10mA - I =0
10 mA +10mA +10mA - I =0
I = 30 mA.
Titta i simulatorn.
Räkna på spänningar
Kirchhoffs spänningslag
Om vi vandrar runt i en sluten krets så kommer potentialen att stiga och sjunka längs vägen och när vi kommer tillbaka till punkten där vi startade så är vi också tillbaka i den potential där vi startade. Ett annat sätt att se på samma sak är att om vi summerar alla potentialförändringar längs vägen så blir summan noll.Exempel 1
Beräkna spänningen U1 och U2 samt potentialerna i P1, P2, P3 och P4.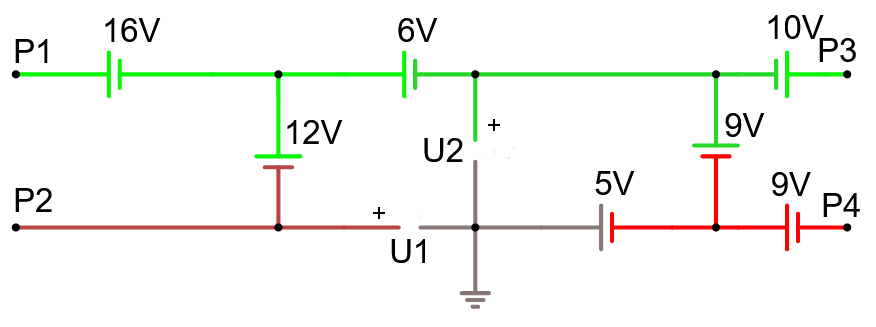
Vi vandrar runt i sådana slingor där vi enbart har 1 obekant. T.ex.
+U2 - 9V + 5V = 0
U2 = 9V - 5V = 4V
Nu när vi vet U2 kan vi även skriva en ekvation för U1 och P1, P2, P3 och P4
U2 + 6V - 12V -U1 = 0
U1 = U2 - 6V = 4V - 6V = -2 V
P1 = U2 + 6V + 16V = 4V + 6V + 16V = 26V
P2 = U1 = -2V
P3 = U2 + 10V = 4V + 10V = 14V
P4 = -5V -9V = -14V
Titta i simulatorn.
Exempel 2
En snabb repetition igen! Strömmen går genom resistorn från högre potential till lägre. Spänningen faller över resistorn.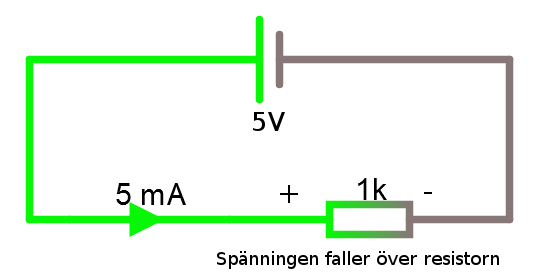
Okej till exemplet. Vi vill räkna ut U.
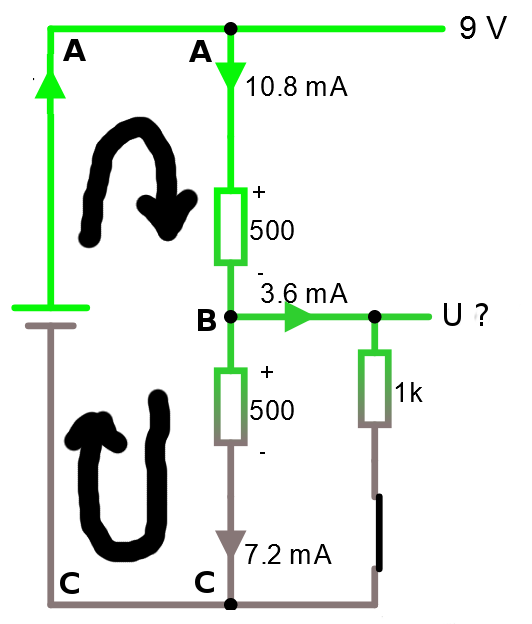
Riktningen och polariteten är jätteviktigt. Spänningen faller över resistanserna i strömmens riktning.
Spänningen +CA -CB -BA = 0 (dvs "Kirchhoffs spänningslag")
CA = 9 volt och BA = 500 Ω * 10.8 mA = 5.4 volt. Om vi dessutom byter ut CB mot U (eftersom det är samma sak i schemat) så får vi
+9 -U -5.4 = 0
U = 3.6 volt
Detta stämmer med räkningar i tidigare exempel ovan.
Exempel 3
Räkna ut U1 och U2 i nedan. Om vi resonerar lite först. För att räkna ut U2 så måste vi veta strömmen genom 1K -resistorn, dvs I1. Vi kan börja med Kirchhoffs strömlag och enkelt räkna ut I1. Alla strömmar in i knutpunkten är lika stort som alla ut.I1 = 2.77 mA - -1.85 mA = 2.77 mA + 1.85 mA = 4.62 mA
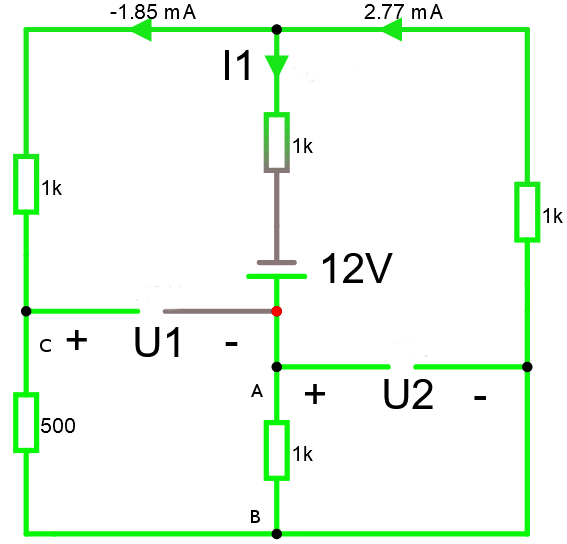
Nu när vi vet att I1 = 4.62 mA kan vi räkna ut U2.
U2 = I1 * 1KΩ = 4.62 mA * 1000 = 4.62 volt.
För att räkna ut U1 kan vi vandra runt i slingan A-B-C. Låt säga potentialen i A är noll (vi har vårt minus där för U1 så det är passande, då får vi rätt tecken på U1). Då går vi med strömmen till B, dvs potentialen i B är -4.62 Volt. Sedan vi mot strömmen och spänningen ökar då med 500 Ω * -1.85 mA (eftersom strömmen är negativ blir det i praktiken en minskning). Dvs;
U1 = -4.62 V + (- 500 * 0.00185) V = -4.62 V -0.926 = -5.54 V
Kirchhoffs spänningslag ger oss också att
-U2 + 500* -1.85mA -U1 = 0
U1 = -U2 - 0.926 = -4.62 V -0.926 = -5.54 V
Dvs samma sak. Vi kan tänka i termer av potentialer eller sätta upp en ekvation för slingan enligt Kirchhoff. Det ger samma resultat. Det är egentligen 2 sidor av exakt samma sak. Titta i simulatorn när du räknat ut.
Exempel 4
Säg att det såg ut såhär istället. Vi vet inte värdet på resistansen som U2 ligger över men vi vet lite annat.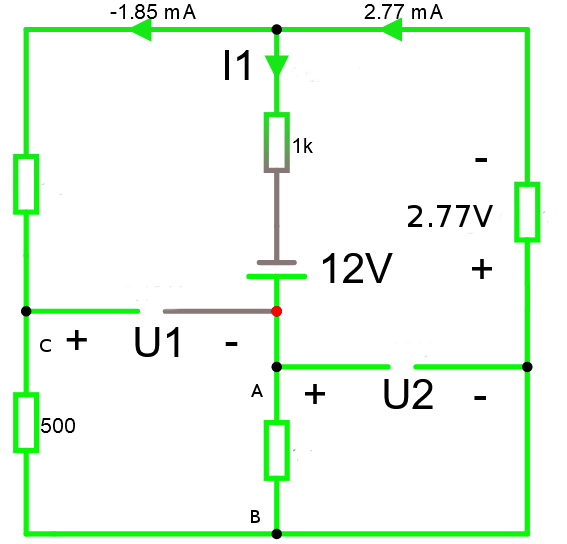
Vi kör Kirchhoffs spänningslag. Eftersom vi ovan räknat ut I1 med Kirchhoffs strömlag vet vi redan I1 i denna uppgift.
-12 V + I1*1000 + 2.77V + U2 = 0
U2 = 12V -I1*1000 - 2.77 = 12V - 4.62V - 2.77V = 4.61V
U1 hade vi sedan kunnat räkna ut på samma sätt som tidigare.
-U2 + 500* -1.85mA -U1 = 0
U1 = -U2 - 0.926 = -4.62 V -0.926 = -5.54 V
Titta i simulatorn.
Exempel 5
Vi vill räkna ut strömmarna I1, I2, I3 i nedanstående krets. Kirchhoffs strömlag ger oss ett samband mellan dessa, nämligen att I1 + I2 = I3. Vi upptäcker efter att ha funderat en stund att det finns inget uppenbart enkel sätt att börja nysta i detta.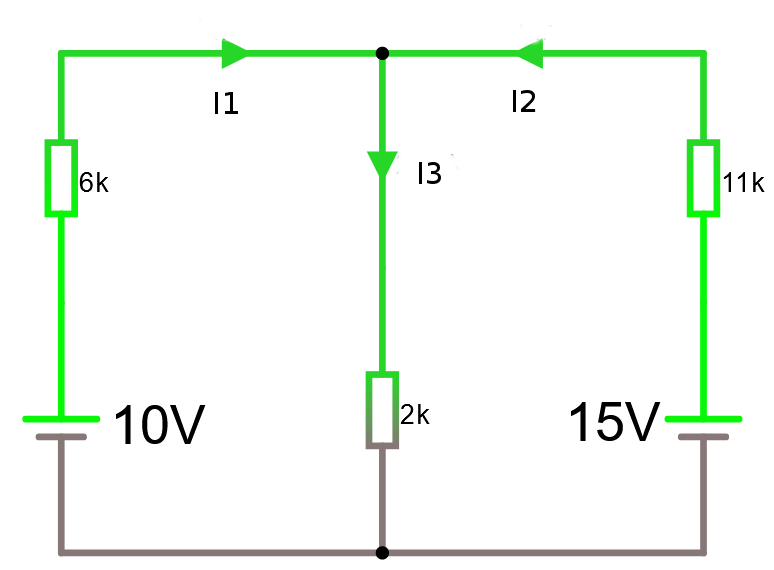
Vi måste börja sätta upp ekvationer för det vi vet och hoppas att vi får lika många ekvationer som obekanta.
Maskanalys / Slinganalys
Vi kan lätt indentifiera 2 slingor och kan sätta upp 2 ekvationer för dessa. Maskanalys innebär att vi tänker oss en ström medurs Ia i den ena maskan och Ib för den andra.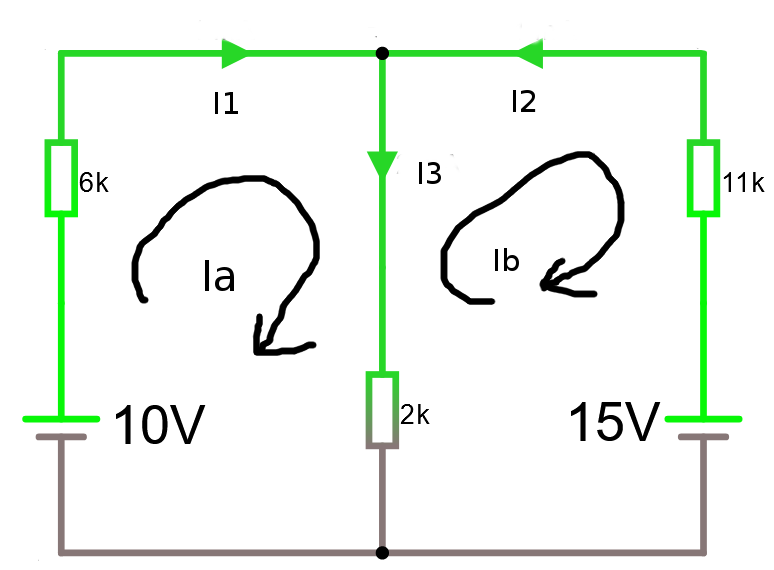
Vi sätter upp ekvationer för dessa 2 slingor givet våra påhittade strömmar Ia och Ib.
(1)
10V -6k * Ia - 2K*(Ia - Ib) = 0
10V - 6K * Ia - 2K*Ia + 2K*Ib = 0
10V - 8K * Ia + 2K*Ib = 0
(2)
-2K*(Ib - Ia) - 11 K*Ib - 15V = 0 (OBS vi följer alltså Ib 's riktning)
-2K*Ib + 2K*Ia - 11K*Ib - 15V =0
-13K*Ib+2K*Ia -15V = 0
-52K*Ib+8K*Ia -60V = 0 (multiplicerar med 4)
8K*Ia = 60V + 52K*Ib
Poängen med att multiplicera med 4 ovan är att vi då enkelt kan slå samman (1) och (2) i ekvation (3)
(3)
10V - 8K * Ia + 2K*Ib = 0
10V - (60V + 52K*Ib) + 2K*Ib = 0 (vi sätter in (2))
10V - 60V - 52K*Ib + 2K *Ib = 0
- 50V - 50K*Ib = 0
Ib = -50V / 50K = -1 mA
Nu kan vi enkelt räkna ut Ia också genom att ta (3) och t.ex. (2) som blir (4)
(4)
8K*Ia = 60V + 52K*Ib
Ia = (60V + 52K*Ib)/8K = (60V - 52V) / 8K = 1 mA
Så vi vet att Ia = 1 mA och Ib = -1mA nu.
Eftersom I1 = Ia och I2 = -Ib så vet vi vidare att I1 = 1 mA och I2 = --1mA = 1 mA.
I3 = I1 + I2 =1 mA + 1 mA = 2mA.
Studera kretsen i simulatorn.