Potentialer i en krets
Referensriktningar och polaritet
En inte så svår men mycket viktig grej att lära är att hålla reda på strömmens riktning och spänningens polaritet. Om man slarvar här kommer man trötta ut sig själv med alla knasiga fel som uppstår längre fram (matte, fysik & elektronik handlar egentligen bara om att vara noga och under resans väg undvika fel, resten är enkelt).Strömmen genom en resistor är riktad från högre potential (+) till lägre potential (-). Spänningen faller över resistorn.
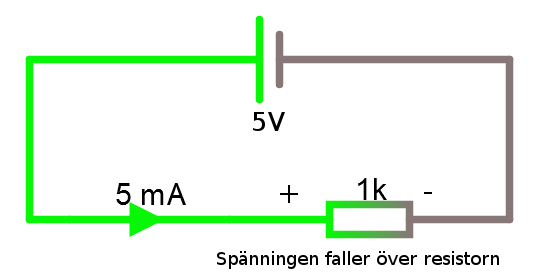
Potentialer
Om vi lägger in en nollreferens - ett jordplan - kan vi prata om potentialer. En potential är spänningen mellan jordplanet och en viss punkt i kretsen. Dvs, som om vi applicerat en voltmätare med minus på jordplanet och sedan testar olika punkter i kretsen och läser av spänningen. Detta innebär ju att spänningen i kretsen på vissa ställen kan bli negativa. Sätter vi t.ex. jordplanet på spänningskällans positiva sida, så kommer de flesta potentialer uppenbart att bli negativa när vi mäter. Är du med på detta?1. Räkna ut potentialer i A, B och C
Vi har ett jordplan vid C, som därför är 0V (per definition). Potentialen vid A höjs med batteriets spänning. För att ta reda på potentialen i B, så behöver vi räkna ut strömmen i slingan.I = U / R = 9V / (4K+8K) = 0.75 mA.
Det betyder då att spänningen faller (spänningen faller i strömmens riktning över en resistor) från A till B med 4K x 0.75 mA. Eller om man så vill, stiger (spänningen stiger mot strömmen över en resistor) från C till B med 8K x 0.75 mA.
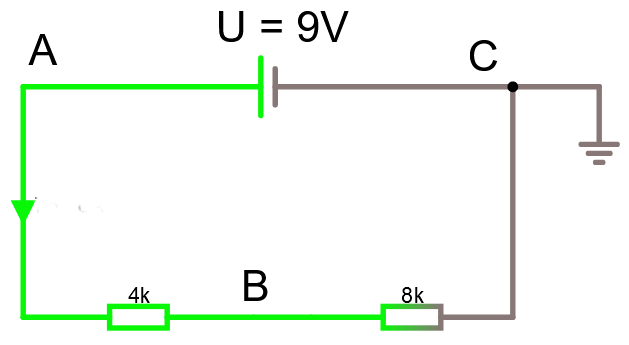
Svaret är alltså; A = 9v, B = 6v, C = 0v. Titta i simulatorn.
2. Räkna ut potentialer i A och B
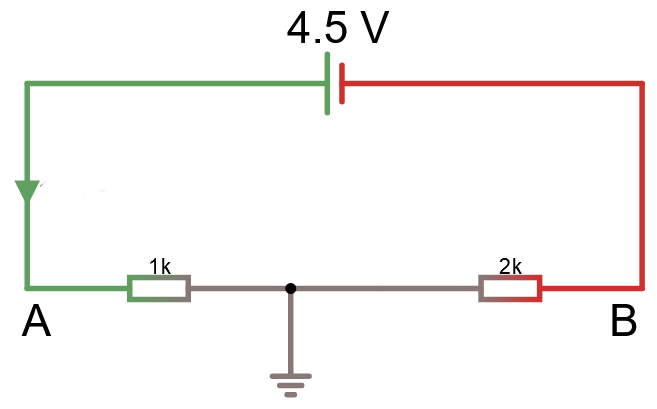
Tänk på var noll-potentialen ligger här och hur potentialen förändras när du vandrar över resistorerna. Börja med att räkna ut strömmen i slingan.
I = U / R = 4.5 / (1K+2K) = 0.15 mA
Tänk sedan på att spänningen faller över en resistor i strömmens riktning. Det innebär också att spänningen stiger mot strömmens riktning. Titta i simulatorn när du löst uppgiften för att se om du fick rätt.
3. Räkna ut potentialer i A och B före och efter brytaren är tillslagen
Om det inte flyter någon ström, då sker inget spänningsfall över något resistor.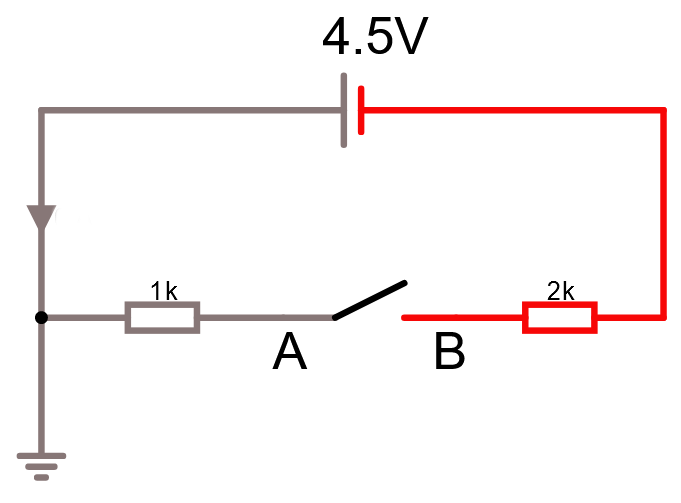
Räkna först ut strömmen och tänk sedan på var du har noll -potentialen i schemat. Titta i simulatorn när du löst uppgiften.
4. Räkna ut potentialer i A och B
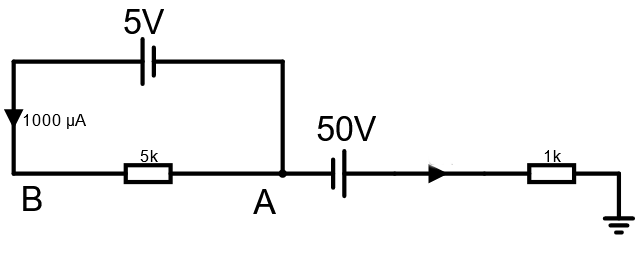
En uppgift kan försöka lura dig. Tänk på vad strömmar går och inte. Potentialer kan lyftas eller sänkas men det måste inte nödvändigtvis gå någon ström. Titta i simulatorn när du löst uppgiften.
5. Räkna ut spänningar och strömmar
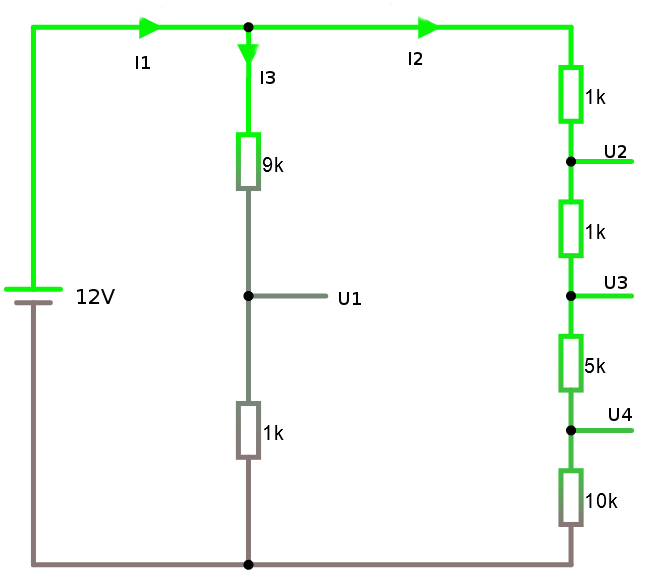
Tips är att räkna ut först räkna ut I3 och I2 genom att dividera spänningen med de seriekopplade resistanserna. Sedan kan du räkna ut spänningarna över respektive motstånd. Titta på facit i simulatorn efter att du löst uppgiften.
6. Räkna ut U samt I1
Nu när vi lärt oss parallellkoppla kan vi räkna ut nedanstående. Vad blir strömmen I1 i kretsen nedan om vi slår till switchen ?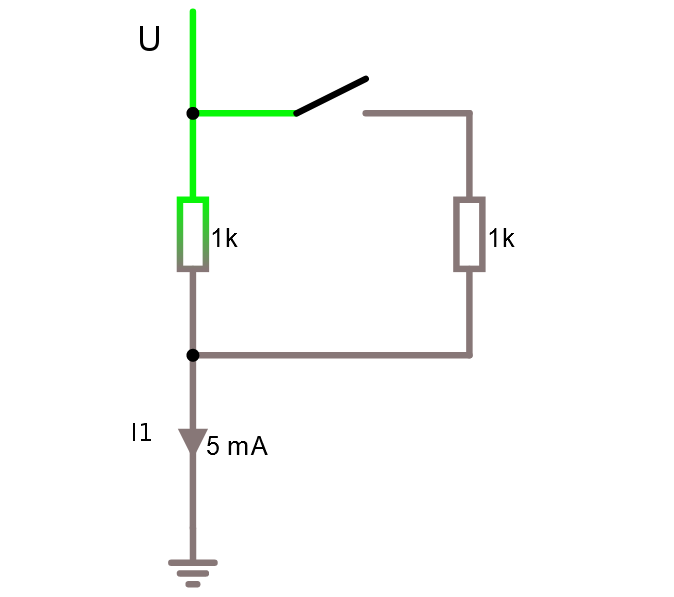
För att räkna ut detta kan man t.ex. först räkna ut U. Då vet vi att eftersom strömmen genom 1K -resistorn är 5 mA så är spänningen över resistorn U = R*I = 1000 * 0.005 = 5 volt. Dvs U = 5 volt.
Om vi slår till switchen får vi 2 stycken parallellkopplade 1K -resistorer.
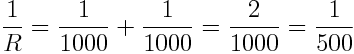
Vi inverterar båda sidor och får fram R = 500 Ω. Vi använder ohms lag för att räkna ut strömmen med I = U/R = 5 / 500 = 0.010 A = 10 mA.
Klicka i och ur switchen och se vad som händer.
Spänningsdelare
En väldigt vanlig konstruktion i elektroniska kretsar är en spänningsdelare. En variabel spänningsdelare vi ofta kommer i kontakt med är en potentiometer.
Och såhär fungerar en potentiometer.
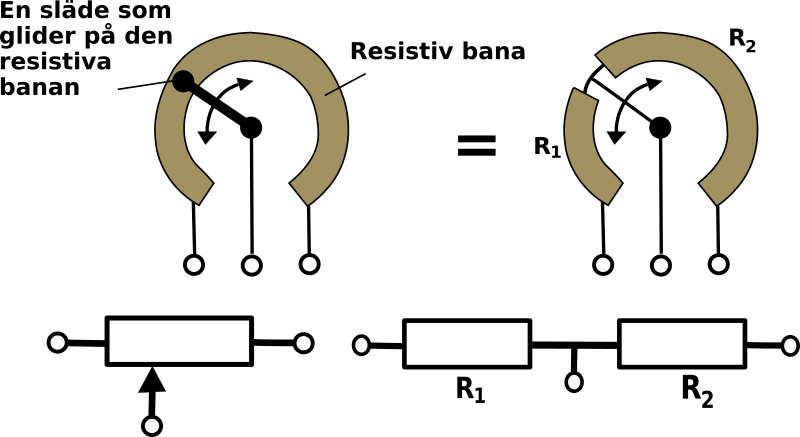
En snabb repetition. Strömmen går genom resistorn från högre potential till lägre. Spänningen faller över resistorn.

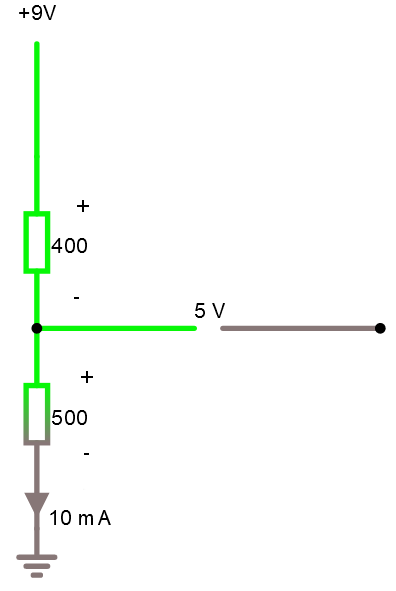
En spänningsdelare "delar" spänningen i 2 eller flera delar. Se nedan schema. Om strömmen genom 500 Ω -resistorn är 10 mA så blir spänningen över densamma U = R * I = 500 Ω * 0.010 A = 5 V. Samtidigt blir spänningen över det övre motståndet U = R * I = 400 Ω * 0.010 A = 4 V. Spänningen 9 volt har alltså "delats" i 4 v och 5 v. Notera i nedan hur spänningen faller över det första motståndet med 4 volt och sedan faller ytterligare 5 volt. Det ligger alltså 5 volt över den undre resistansen och 4 volt över den övre.
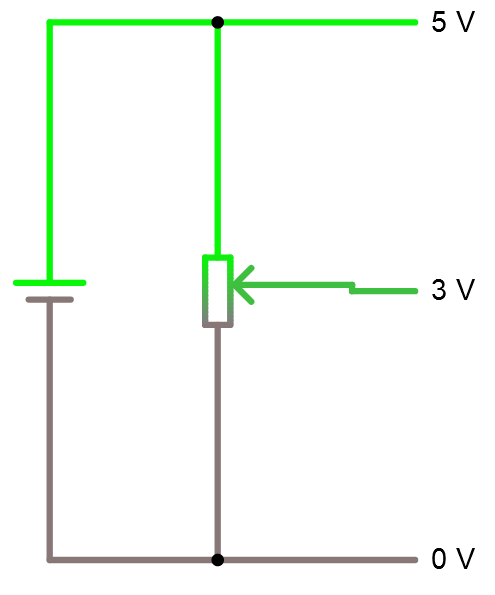
Vi kan också skapa en spänningsdelare med en potentiometer. Detta är väldigt användbart om om man tänker sig att vi vill få in ett analogt värde i en A/D -omvandlare i en mikrokontroller. Sen kan vi läsa av detta analoga värde (på t.ex. en arduino) från potentiometern på en skala 0-1023 i mjukvaran förutsatt att spänningen är 0-5 volt.
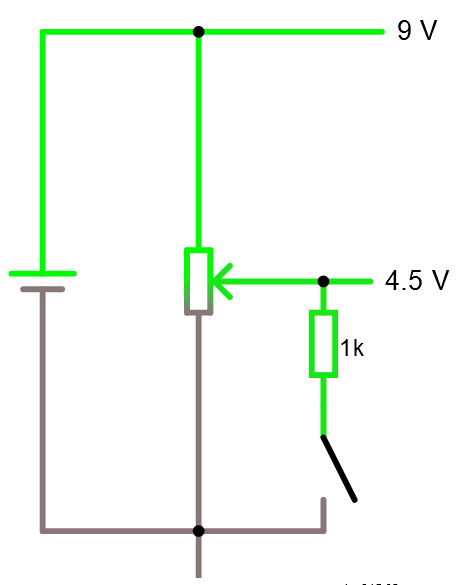
En spänningsdelare kan inte användas hur som helst. Begrunda nedan uppkoppling en stund. Vi har 9 volt över en 1K -potentiometer som vi har skruvat på så att den står i mitten och får därför ut 4.5 volt.
Om vi nu kopplar in lasten så händer detta.
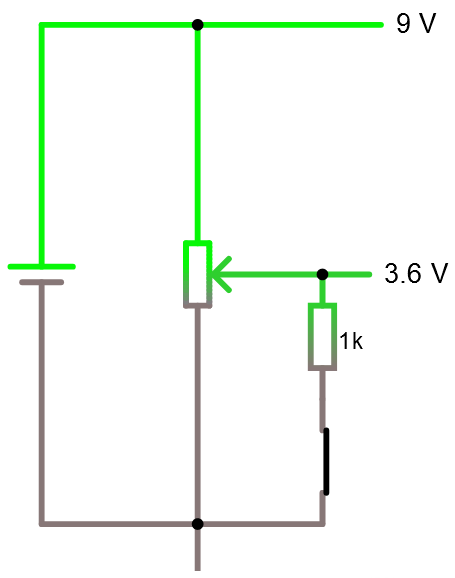
Det är ju förstås så att eftersom vår last har en resistans och drar ström så förändras hela kalkylen när vi kopplar in lasten. Om potentiometern står i mitten ser det först ut såhär. Strömmen är först I = U / R = 9 / 1000 = 9 mA.
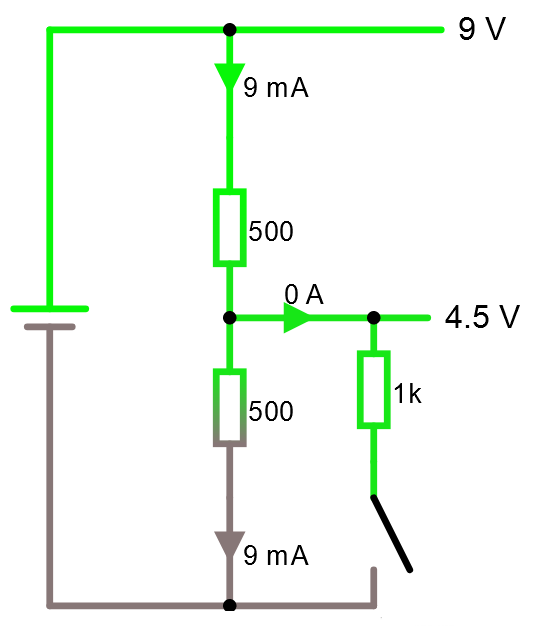
Men när vi kopplar in lasten så drar även lasten ström. Detta förändrar spänningsdelaren delning av spänningen eftersom den undre resistansen blir 1/ R = 1/500+1/1000 vilket ger R = 333 Ω. Dvs vi får en spänningsdelning mellan 500 Ω och 333 Ω. En ström I = U / R = 9 / 833 = 10.8 mA.
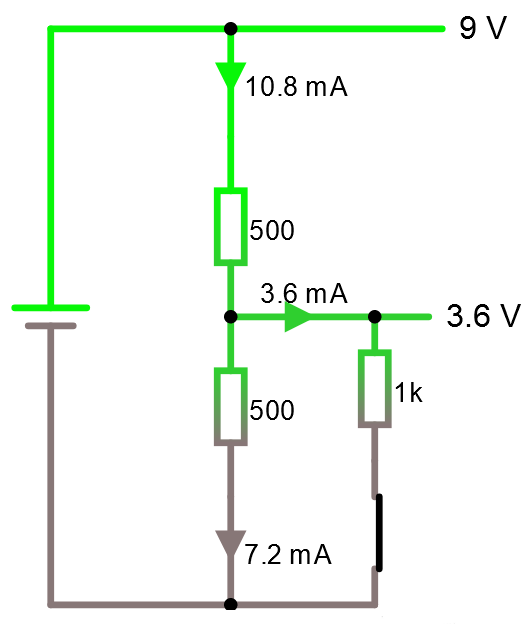
Spänningen ut blir U = R * I = 333 Ω * 10.8 mA = 3.6 volt.
Spänningsdelare är alltså helt kassa om det man vill driva drar en ström i närheten av den ström som flyter i spänningsdelaren. Om strömmen däremot är väldigt liten i förhållande till strömmen i spänningsdelaren så fungerar en spänningsdelare utmärkt och konstruktionen är därför vanlig inne i kretsar.
Exprimentera med ovan spänningsdelare i simulatorn.
Håll i minnet hur 10.8 mA ovan delar sig i 3.6 mA och 7.2 mA och notera att 10.8 mA = 7.2 mA + 3.6 mA. Om du uppfattar detta som logiskt och självklart att summan strömmar in i punkten är samma som strömmar ut, då fixar du Kirchhoffs strömlag ganska snabbt.