Karnaughdiagram
Från Karnaughdiagram till kretsschema!
Klicka i Karnaugh-diagrammet för att sätta utsignalerna och ett tänkbart kretsschema ritas upp. Du kan sätta utsignalen till 0 eller 1 och även X för "Dont care".Antal variabler:
Klicka i Karnaughdiagrammet för att sätta utsignaler till 1 eller 0 eller X (dont care).
Ovan ger nedanstående kretsschema.
Poängen med Karnaughdiagram
Poängen med karnaughdiagram kokar ner till att vi människor oftast har ganska lätt att se mönster. Så genom att ordna variablerna i ett smart system, så blir det lättare att få fram hur signalerna kan beskrivas med algebra. Detta är iallafall tanken.Observera att det ofta finns flera olika lösningar, som alla är optimala. Så om du kommer fram till en lösning som inte är samma som på denna sida, så är den troligtvis inte fel utan båda är rätt.
Variabler
Det förekommer en hel del varianter på temat namngivning av variabler i karnaughdiagram. Men det är inget haka upp sig på. Konceptet påverkas inte av detta.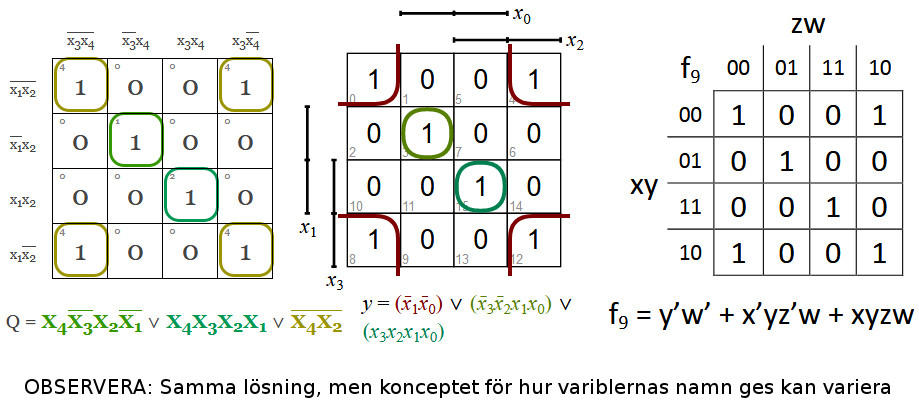
Karnaugh själv verkar föredragit ABCD ...
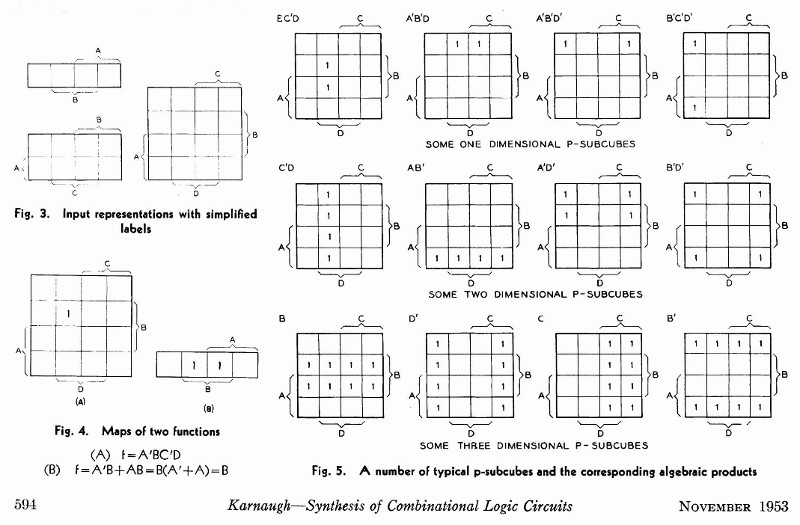
Hoptagningar
Det hela går alltså ut på att ringa runt ettor. I enklaste formen och tyvär sämsta fallet, så går det inte att göra så mycket mer än att ringa runt de ettor som finns.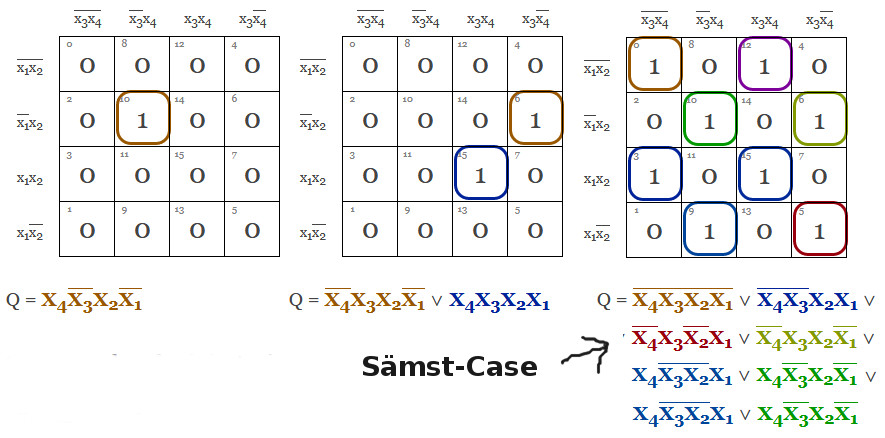
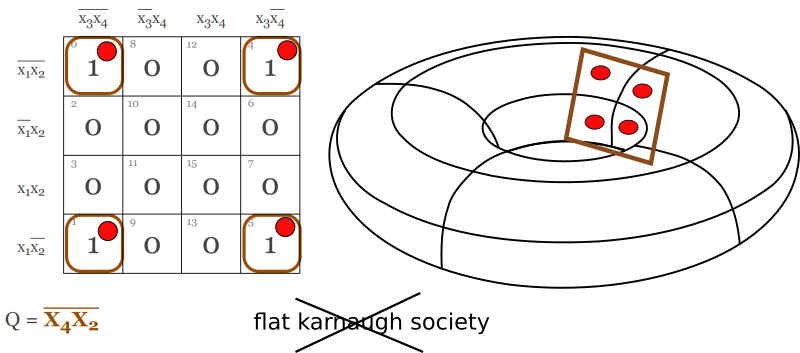
En ensam 1:a som inte täcks in av någon annan ring, därför att det helt enkelt inte går att göra, det kallas väsentlig primimplikator. Vi har alltså inte något val här utan måste plocka med denna. Det blir genast trevligare om ettorna ligger brevid varandra horisontellt eller vertikalt. Då kan vi göra en ring runt dessa 2 stycken. Notera att en variabel (en dimension) försvinner. En viktig användbar grej här, det är att karnaughdiagrammet är ingen platt värld. Du trillar inte över kanten och dör, utan diagrammet fortsätter på andra sidan. Så du kan göra en hoptagning som rör sig över kanten till andra änden.
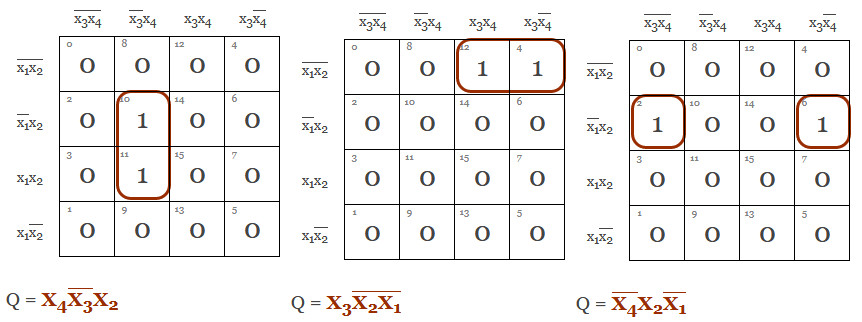
Detta blir tydligare användbart om vi har fler 1:or att bunta ihop.
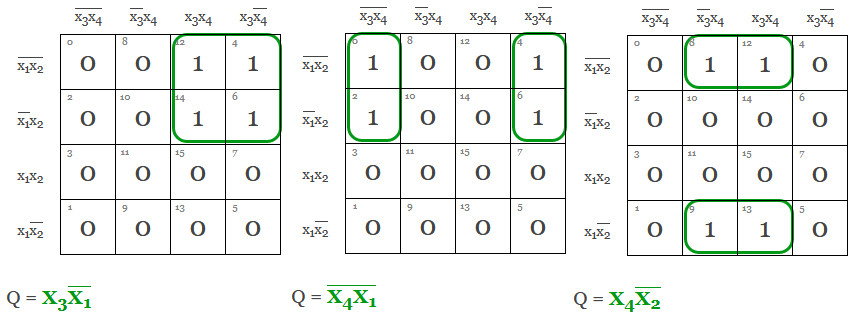
Fler 4:or som vi kan bunta ihop...
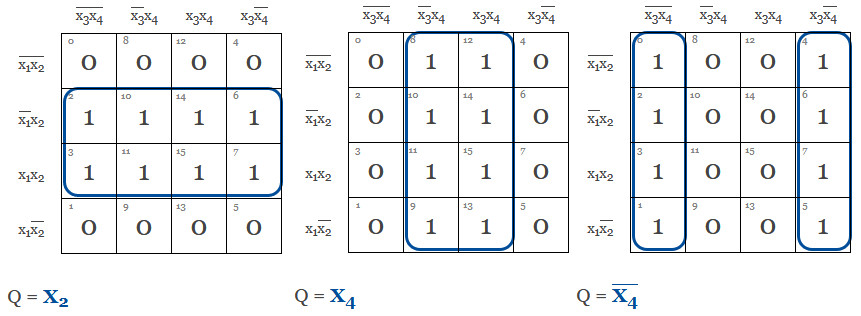
Har vi tur kan vi para ihop 8 stycken. Även dessa grupper kan "trilla över kanten" och dyka upp på motsatt sida.
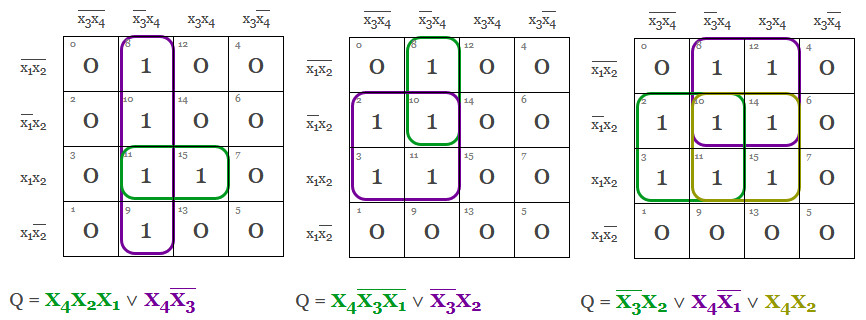
Oftast är det inte så enkelt att vi har en fin grupp som går att para ihop. Då måste vi bygga ett lappverk av hoptagningar. Den enda regel som gäller i detta krig är: Så stora ytor som möjligt! De kommer överlappa varandra, vilket de också ska! Vi får då färre variabler att jobba med vilket är vad vi önskar.
Dont care!
Ibland har vi signaler vars värde inte spelar någon roll, s.k. "dont care" eller "x" eller "-". Detta är användbart då det oftast leder till enklare nät.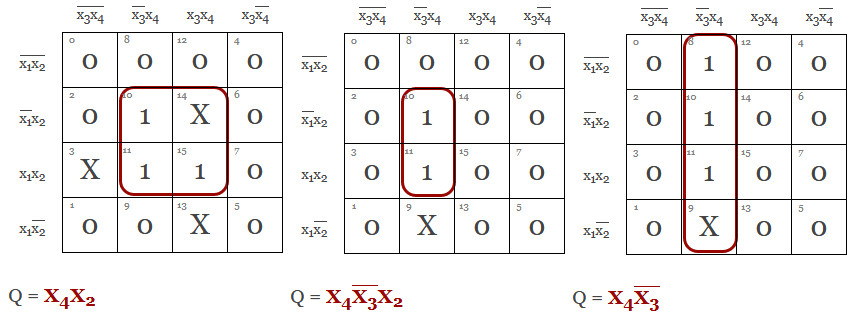
Vi kan nämligen själva välja om dont care ska ingå i ett mönster eller inte. Förslagsvis väljer vi att hantera detta så att största möjliga ytor täcks in eftersom det ger kortaste beskrivningen av signalerna.
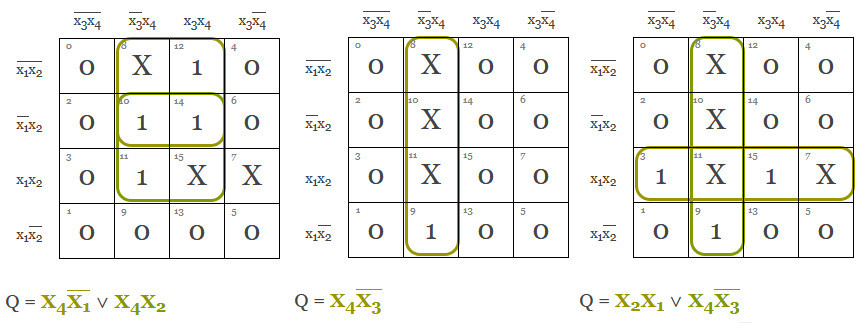
Fler variabler än 4:a
Om vi har 5 variabler så kan vi visualisera det såhär. Fortfarande gäller samma regler fast nu i 3 dimensioner. Om du väljer 5 eller 6 variabler överst på sidan så kan du labba och testa.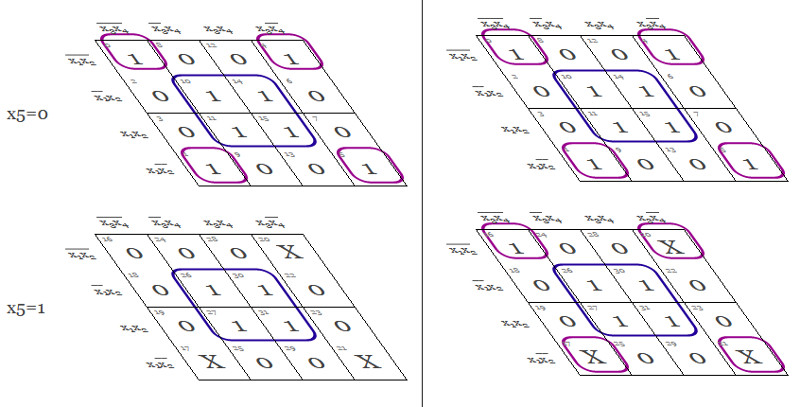
Några regler betraktade med karnaugdiagram.
Absorption
x ∨ x∧y = x

Konsensus
x∧y ∨ x∧z ∨ y∧z = x∧y ∨ x∧z
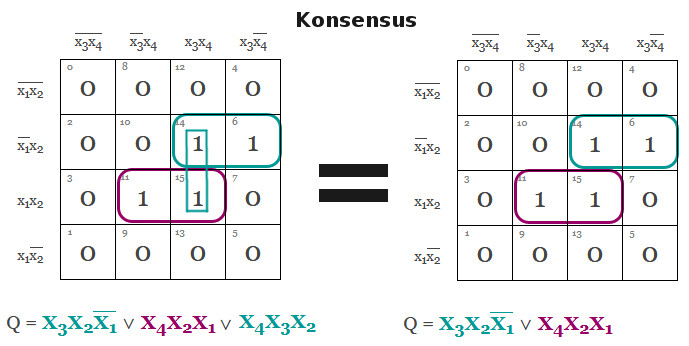
Lycka till med tentan!
