Quine McCluskey
Från sanningstabell till kretsschema!
Klicka med musen i den grå kolumnen Q i sanningstabellen nedan för att sätta utsignalerna för Q = f(Xn,...,X2, X1), så räknas funktionen f ut med Quine McCluskey's algoritm och ett tänkbart kretsschema ritas upp. Du kan sätta utsignalen till 0 eller 1 och även X som betyder "Dont care". Antal variabler:Klicka i den grå kolumnen Q för att sätta utsignaler.
 |
Ovan ger nedanstående kretsschema.
Lite terminologi
Ibland används ordet "primimplikatorer" och ibland "primära implikatorer" och ibland något annat. Ibland skriver man "essentiell minterm" och ibland "väsentlig minterm" och även här betyder det samma sak. Primtäckning brukar det kallas om en PI-tabell ger hela lösningen.Quine McCluskey's algoritm
Quine McCluskey's algoritm involverar några steg.1.
Skapa en lista som du kallar ordning 0 med alla termer som blir 1 eller X (dont care).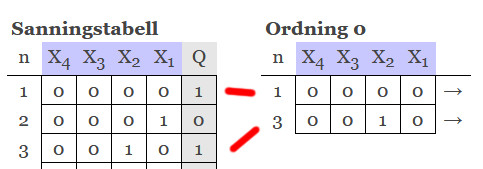
2.
Para ihop ihop termer där enbart en bit skiljer sig åt och placera dessa i ordning 1. Exempelvis så förvandlas paret 1010 och 1011 till 101- och paret 1100 och 0100 förvandlas till -100. Paret --00 och --10 förvandlas till ---0.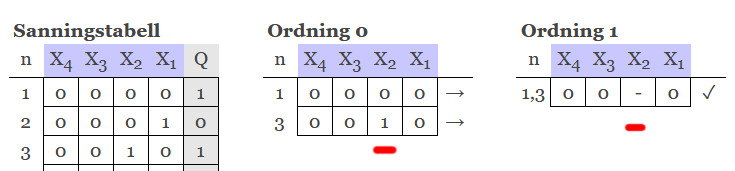
3.
Bygg samtidigt en PI -tabell (PI = primimplikatorer) där alla termer hamnar som inte längre låter sig paras i tidigare tabeller (som blir ensamma kvar). T.ex. går det inte att para ihop 1001 med 0110 eftersom de skiljer sig åt på 2 bitar. Inte heller går det att para -111 med -001 eftersom det också skiljer sig på 2 bitar.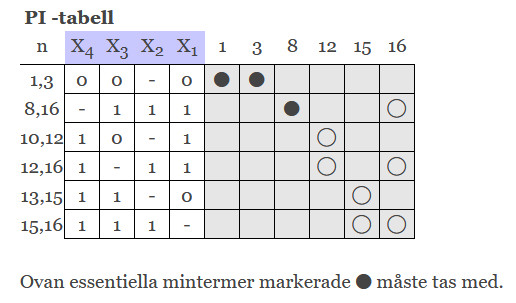
4.
I PI -tabellen kommer man se att vissa termer måste finnas med då de är ensamma om att täcka in vissa bitar. Dessa termer kan man skriva ner och samtidigt stryka från tabellen. Efter att man skrivit ner och strykt alla nödvändiga termer, så kan man göra en ny tabell av det som återstår.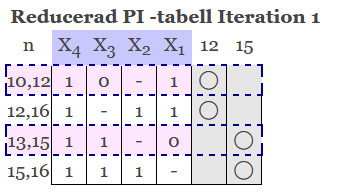
5.
Nu får du med en annan metod plocka ut resterande mintermer. Ofta är det väldigt uppenbart vilka mintermer det handlar om, ibland klurigare. Det finns vanligtvis flera alternativ. Petrick's metod kan hjälpa här, vilket också löser cykliska problem.Exempel 1
Så, efter att ha skapat vår sanningstabell, så flyttar vi över alla mintermer (alla rader där vi har värdet 1 eller X = dont care) till en ny tabell som vi kan kalla ordning 0.Det vi sedan skall göra handlar om att para ihop mintermer där det enbart skiljer på 1 position. På denna position skriver vi ett streck. De som inte kan paras ihop med någon annan minterm, dessa går direkt till PI-tabellen. Här kunde alla paras ihop. Notera att de som parats ihop inte kan paras ihop ytterligare en gång. Det skiljer nämligen på 2 positioner på samtliga och det är enbart par där det skiljer på 1 position som kan paras ihop.
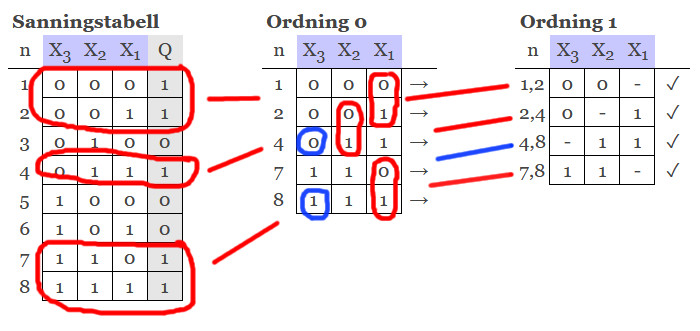
Vi kan alltså inte para ihop mintermerna mer. De vi inte kan para ihop mer stoppar vi in i vår PI-tabell. I denna markerar vi alla variabler en viss minterm täcker. Har vi tur får vi fram några essentiella mintermer, dvs sådana som är absolut nödvändiga. Det är tacksamt eftersom vi då inte behöver tänka. Dessa essentiella ska alltid med. Vi noterar detta och gör samtidigt en ny tabell med de mintermer som blir över, som inte blivit täckta. Här kan det vara mer eller mindre trivialt att plocka ut resterande termer.
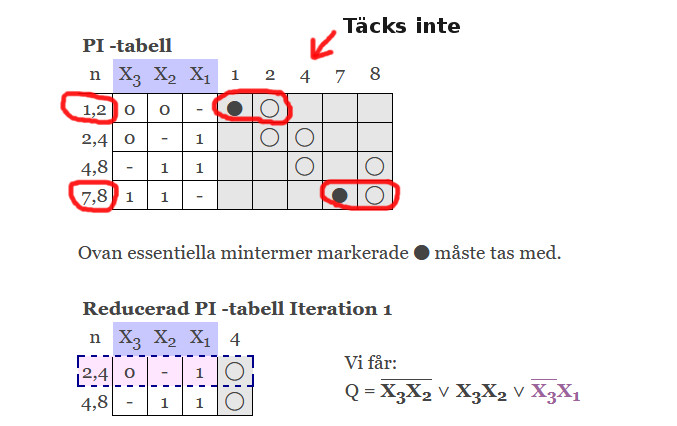
I detta fall är det enkelt. Vi kan välja vilken som helst av 2,4 eller 4,8. Båda gör jobbet med att täcka 4:an.
Exempel 2
Lite större exempel. Vi parar ihop de mintermer där det enbart skiljer i en position. Observera att vi behandlar dont care (X) som en minterm. Vi gör detta fram till PI-tabellen där vi bortser ifrån X. De som inte kan paras ihop skickar vi direkt till PI -tabellen. Här ser vi dock att vi kan fortsätta och para ihop några stycken av de vi redan parade ihop i "ordning 1", så vi får en tabell "ordning 2". I tabellen "ordning 2" kan vi sedan inte para ihop mer, så vi skickar dessa till PI-tabellen.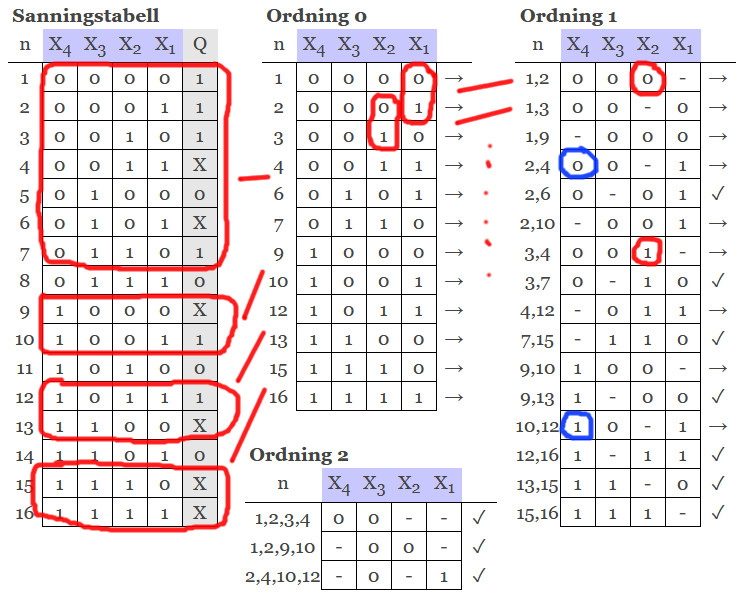
Här ser vi då att vi faktiskt inte har några essentiella mintermer. Det betyder att det finns flera olika lösningar. En sådan lösning verkar vara att använda mintermerna 3,7 och 12,16 samt 1,2,9,10.

Dont care! (X)
Dont care! = X
Hantera X som en 1:a fram till slutet - där du bortser från termen helt.
Hantera X som en 1:a fram till slutet - där du bortser från termen helt.
Det enklaste sättet att snabbt begripa detta är troligtvis att labba lite med dont care i ett Karnaughdiagram.
Komplexitet
McCluskey påstås vara mer praktisk än Karnaugh -diagram när man har väldigt många variabler. Men även här växer komplexiteten med McCluskey's algoritm exponentiellt, med antal variabler. Simulatorn på denna sida har jag knackat ihop i javascript och det är tänkbart att om du väljer många variabler och många X, så kommer det bli väldigt långsamt. Konverteringen till kretsschema kommer även det fallera grafiskt (utrymmeskäl på sidan) om det är för många mintermer. Tanken är mest att åskådliggöra mindre exempel för att lära ut.Lycka till!