Binär kodning
Aritmetik med binära tal
Binärt tal utan tecken (unsigned)
Ett binärt tal består av 1:or och 0:or. Vi tänker oss t.ex. ett 8 bitars tal. Dvs, det är 8 bitar långt. En bit = en etta eller nolla. 8 bitar = 8 stycken 1:or eller 0:or. De olika positionerna har vikter enligt följande.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Det vill säga, ovanstående tal representerar 1+4 = 5.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
Ovanstående tal representerar 1+4+32+64=101
Binärt tal med tecken (signed)
Ett binärt tal med tecken, där envänder vi MSB (den mest betydelsefulla biten) till tecken. En etta (1) betyder minus. Nolla betyder plus.
Detta kallas också teckenbeloppsform (viktigt begrepp). Tänk "tecken + belopp".
| tecken | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Ovanstående är alltså 5, dvs +5 om man så vill. Fem, helt enkelt.
| tecken | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Ovanstående är -5. Ettan i början betyder minus och resterande 7 bitar representerar i detta fall fem.
| tecken | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
Ovanstående har en minus-bit i början. Resterande 7 bitar representerar 64+2=66. Så talet här är -66.
Binärt tal 2-komplement (signed)
Poängen med 2-komplement är att vi använder det vid subtraktion, vilket strax förklaras. För att konvertera till 2-komplement gör såhär:
1. Invertera alla bitar.
2. Lägg till 1.
Låt säga vi vill representera -12 med binär 2-komplement. Vi kan skriva såhär -122k eller något i den stilen.
Vi börjar med 12 ...
| tecken | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
Invertera alla bitar...
| tecken | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Lägg till 1 ...
| tecken | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
Nu har vi -12 på 2-komplementform.
Addition 2 binära tal
Vi gör precis som med 10 som bas, fast nu räknar vi bara från 0 till 1.
Så, om vi vill räkna ut 20 + 20 = 40
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
Subtraktion 2 binära tal
Poängen med 2-komplement, som vi gick igenom ovan, är att vi kan subtrahera 2 binära tal. Det råkar nämligen vara så att A - B är samma sak som A + B2k, dvs där B alltså är på 2-komplementform.
Säg att vi vill räkna ut 20 - 12 binärt. Detta är samma sak som 20 + 122k. Så vi räknar ut 122k vilket vi redan gjort ovan. Sedan är additionen 20 + 122k enkel.
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Vi kommer dock få en C (carry, minnessiffra) utanför som bieffekt också. Men om vi bortser från det en stund, notera att svaret 8 är korrekt. 20 - 12 = 20 + 122k = 8.
Addera med logiska grindar
Halvadderare
Varför kallas det halvadderare? En halvadderare kan enbart lägga ihop 2 stycken bitar, den går inte att koppla ihop med andra adderare för att addera något större tal.
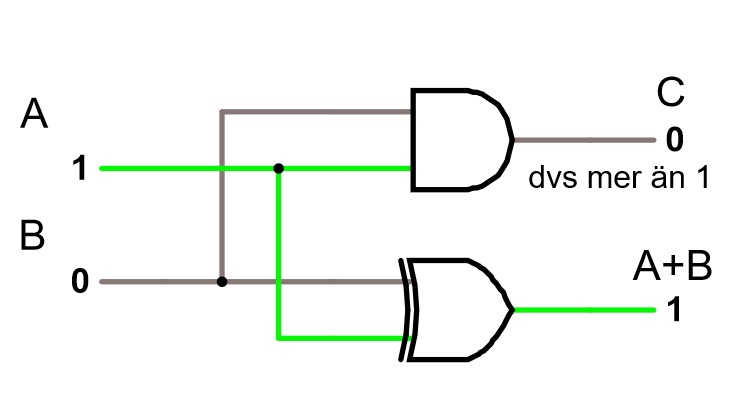
Vi adderar binära tal på samma sätt som alla andra tal.
| A | B | A + B | C (carry, minnessiffra) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Studera en halvadderare i simulatorn.
Heladderare
Heladderaren tar hänsyn till att vi kan ha en ingående carry (minnessiffra), vilket är nödvändigt om vi har många siffror inblandade - eller hur? Detta gör det möjligt att koppla ihop heladderare i lång kjedjor för att addera stora binära tal med många bitar.
| Cin | A | B | A + B + Cin | Cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
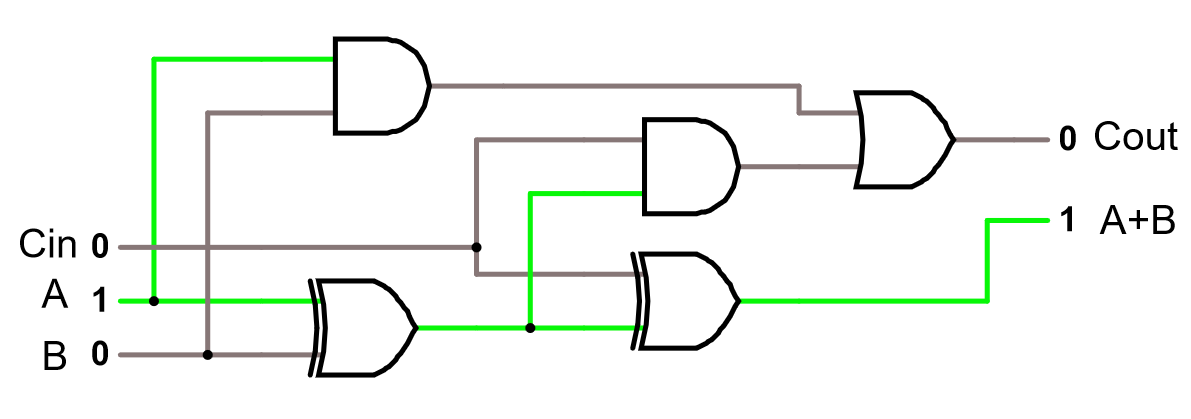
Studera en heladderare i simulatorn. Oftast brukar man tänka sig att man bygger in allt som behövs för en heladderare i ett eget byggblock, som ser ut ungefär såhär:
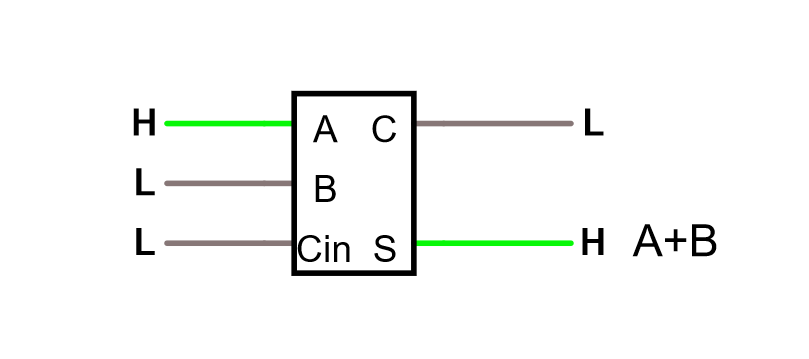
Studera en integrerad heladderare i simulatorn.
Heladderare 4 bitar
Så, vi kan sedan bygga ihop sådana här block så att vi kan addera binära tal med många bitar. Precis som vi lärt oss addera tal i matematiken, så flyttar vi vidare eventuell minnes-siffra till nästa tal i additionen. Så utgående carry från första additionen, blir ingående carry på andra additionen. osv.
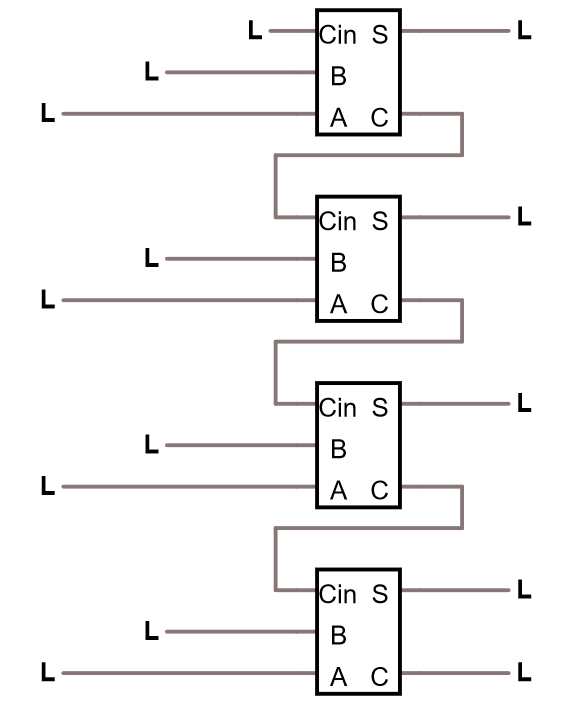
Addera 2 stycken 4-bitars tal
Subtraktion med logiska grindar
Vi kan beräkna A - B genom att först omvandla B till 2-komplement. När vi har B i 2-komplementform, så är A + B2k = A - B. Dvs vi beräknar A + B2k vilket är samma sak som A - B.
Vi lärde oss att 2-komplement, det fixar vi genom att
1) invertera alla bitar
2) lägga till 1.
Hur gör ett kretsschema av denna teori?
Invertera logiska signaler
Så, hur sjutton ska vi invertera logiska signaler? Skåda XOR -grinden!
Vi kan sätta en av de 2 ingångarna på XOR till 1 och då kommer den alltid invertera. Sätter vi samma ingång till 0, så inverterar den inte.
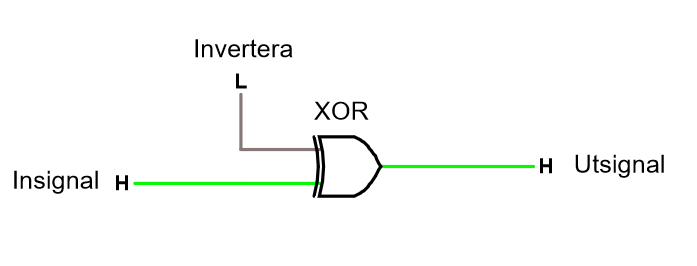
Testa själv invertera med xor.
Hur lägger vi till 1 ?
Mycket enkelt! Vi sätter helt enkelt ingående C (carry, minnessiffra) till 1. Japp, thats it. Case closed. Job done.
Subtraktion 4 bitar med heladderare + 2-komplement
Ett återstående problem var att utgående carry blir inverterad, när vi gör subtraktion. Men vi kan inverter tillbaka den med en xor där också. Vi kan alltså bygga en subtraherare såhär.
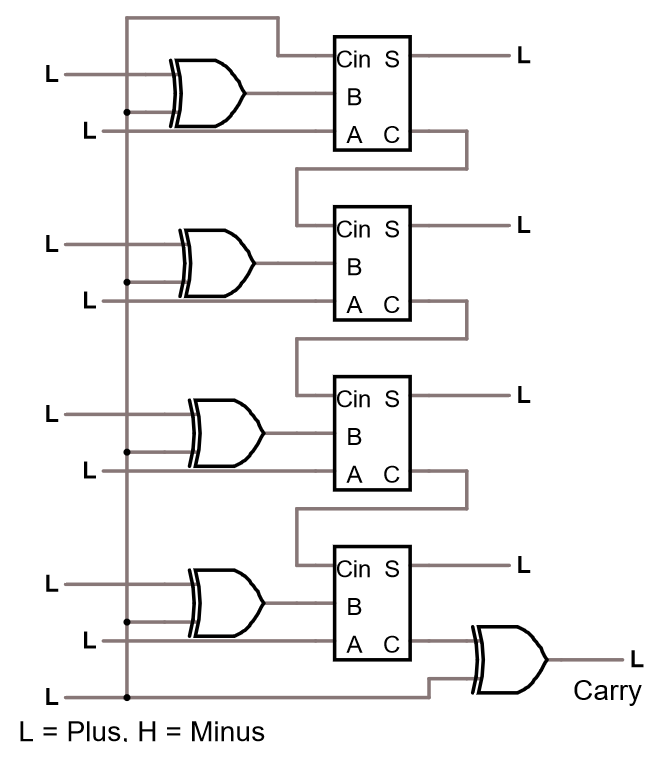
Testa att subtrahera 2 stycken 4-bitars tal. Det går också att ändra operation mellan plus och minus.
En liten miniräknare med plus och minus, 4 bitar
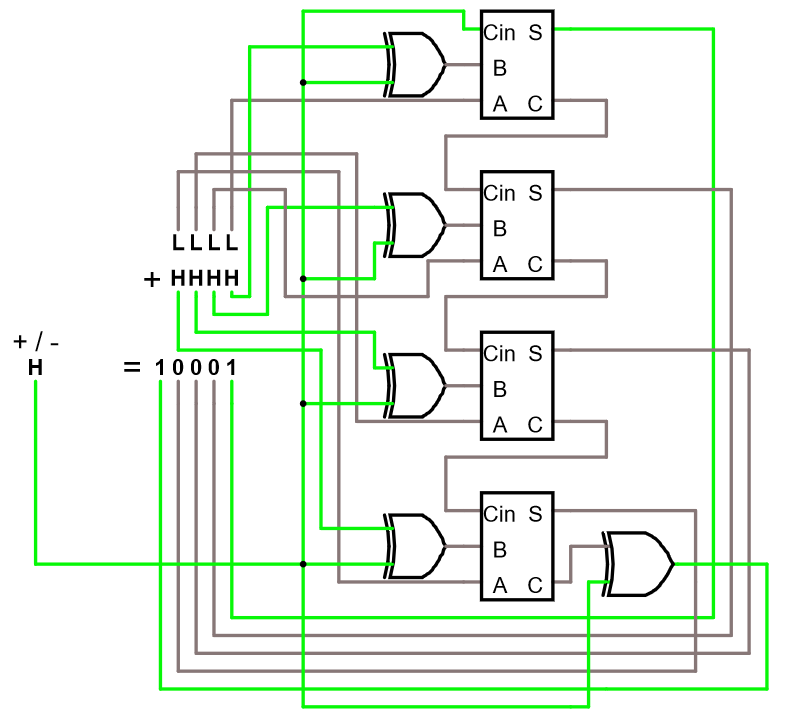
En liten 4-bitars miniräknare. Välj plus eller minus. Sätt bitarna som skall adderas eller subtraheras.
Hexadecimal form
Så, i decimal form representerar nedan binära tal 64 + 32 + 4 + 1 = 101
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
Vi kan också betrakta detta på hexadecimal form såhär...
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
Vi tittar på talet i grupper om 4 bitar och får då 65. Det binära talet ovan, 01100101 är alltså decimalt 101 och hexadecimalt 65.
Ett exempel till:
| 8 | 4 | 2 | 1 | 8 | 4 | 2 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
Hexadecimalt räknar vi 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Så ovan binära tal 11101111 blir alltså hexadecimalt EF.