Räkna på kretsar med python
Python är framtiden. Språket letar sig in överallt, datorn, mobiltelefonen, miniräknaren. Nu kan du tom programmera arduino med python om du vill!Pythonkod för serie och parallell -koppling
Med väldigt lite kod kan vi i Python bygga ett kraftigt verktyg som hjälper oss räkna på kretsschema. Du kan snickra på detta bibiotek själv.
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
Thats it!
Med ovan kod kan du sedan knappa in dina kopplingsschema. Låt oss ta ett enkelt exempel, som förstås inte behöver någon pythonkod egentligen, men för att förklara konceptet.
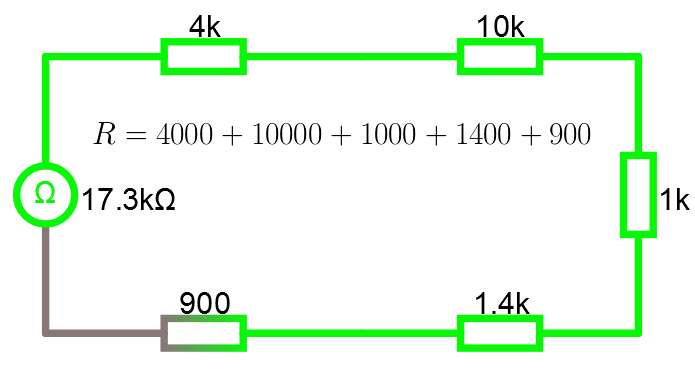
Öppna seriekopplingen i simulatorn.
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
R = serie(4000,10000,1000,1400,900)
print(R)
Seriekopplade resistanser läggs in i funktionen serie( ... )
Har du ingen python -räknare, mobil eller dator kan du alltid komma åt python-rummet från mobil, platta eller dator. Klicka sedan på editor, kopiera in kod och klicka kör.
Studera resultatet: Seriekopplade resistanser. Klicka på kör.
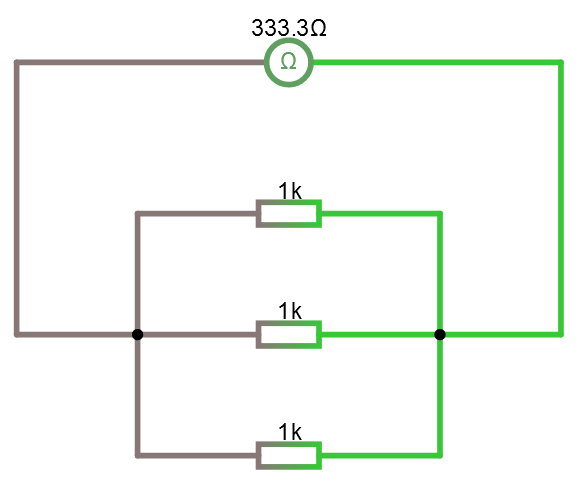
Parallellkoppling av resistanser
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
R = parallell(1000,1000,1000)
print(R)
Parallellkopplade resistanser läggs in i funktionen parallell( ... )
Studera resultatet: Parallellkopplade resistanser. Klicka på kör.
Serie + Parallellkoppling
Det går förstås att kombinera serie och parallellkoppling.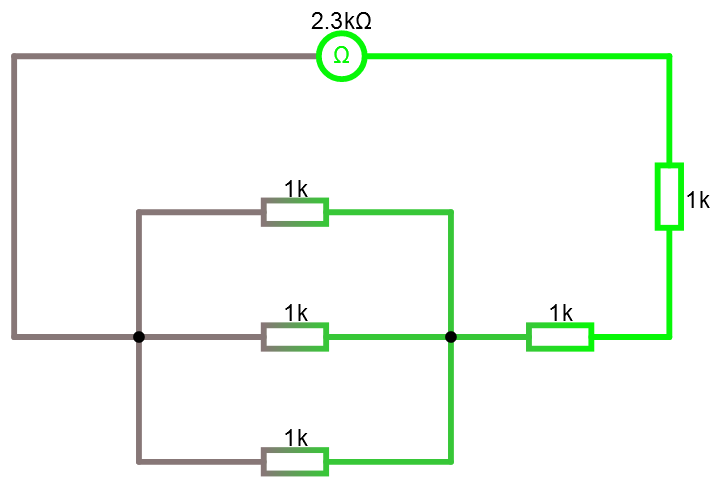
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
R1 = serie(1,1,parallell(1,1,1))
print(R1)
Seriekopplade resistanser kan läggas in som argument till parallellkopplade och vice versa.
Studera resultatet: Serie och parallellkopplade resistanser. Klicka på kör.
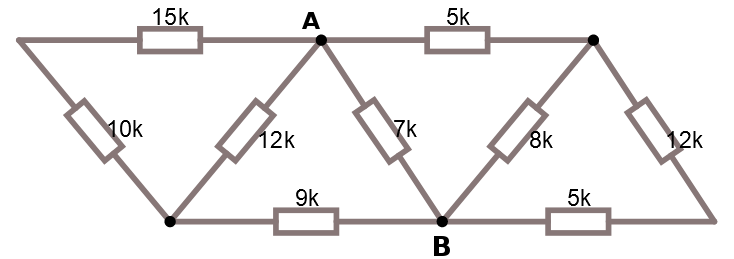
Avancerat exempel
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
R1 = parallell( serie(parallell(serie(15,10),12),9),
7,
serie(parallell(serie(12,5),8),5))
print(R1)
Studera resultatet: Serie och parallellkopplade resistanser. Klicka på kör.
Resistanser på ett kretskort
Vad är resistansen mellan A och B nedan?
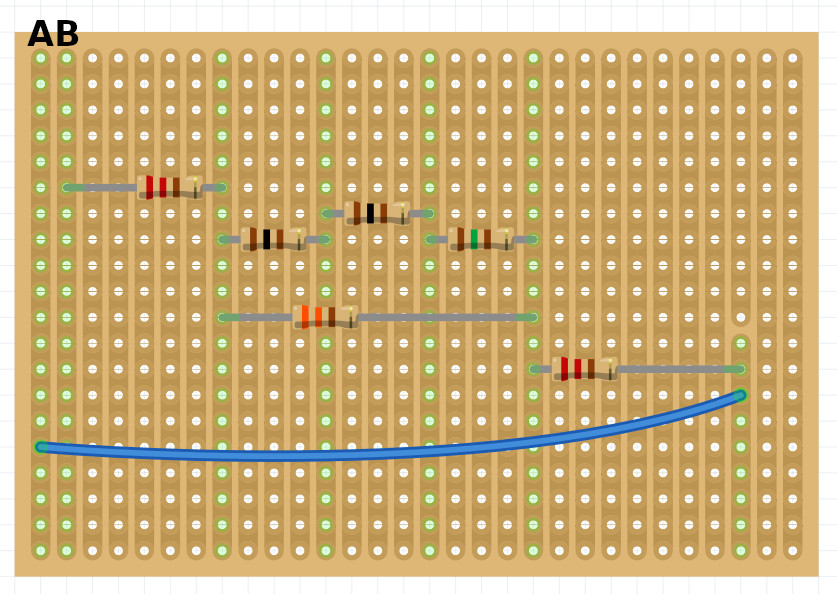
Vi kan bygga ut vårt bibliotek lite, så kan vi även knappa in färgkodade resistanser. Vi lägger till funktionen farg( .. ) som vi kan använda för att ange en resistans istället för ett värde.
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
def farg(*farger):
res = 0
i = 0
v = 0
ant_band=len(farger)
for farg in farger:
i = i + 1
match farg:
case "brun":
v = 1
case "röd":
v = 2
case "orange":
v = 3
case "gul":
v = 4
case "grön":
v = 5
case "blå":
v = 6
case "lila"|"violett":
v = 7
case "grå":
v = 8
case "silver":
v = -2
case "guld":
v = -1
if(ant_band == 3):
if(i==1):
res = res + v*10
if(i==2):
res = res + v*1
if(i==3):
res = res*10**v
if(ant_band == 4):
if(i==1):
res = res + v*100
if(i==2):
res = res + v*10
if(i==3):
res = res + v
if(i==4):
res = res*10**v
return(res)
R = serie(
farg("röd","röd","brun"),
parallell( farg("orange","orange","brun"),
serie( farg("brun","svart","brun"),
farg("brun","svart","brun"),
farg("brun","grön","brun"))),
farg("röd","röd","brun"))
print(round(R),'Ω')
Studera resultatet: Serie och parallellkopplade resistanser. Klicka på kör.
Uppkopplingen i elkretssimulatorn.
Växelström?
Japp! Det går ju också vet du! Vi kan räkna på växelströmskretsar med spolar och kondensatorer.
Reaktanser
Om vi redan har komponenteras värden som reaktanser, så ser det ut såhär.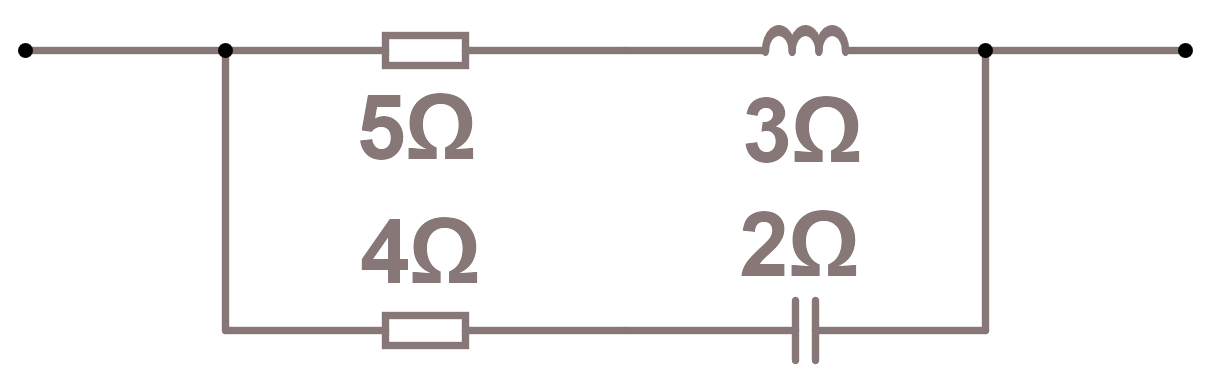
Vi behöver lite fler funktioner i koden eftersom vi räknar med komplexa tal.
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
def R(r):
return complex(r,0)
def I(z):
return complex(0,z)
def C(z):
return complex(0,-z)
def arg(C):
alfa = math.atan(C.imag/C.real)
return(math.degrees(alfa))
def iround(C,d):
return(complex(round(C.real,d),round(C.imag,d)))
z = parallell(serie(R(5),I(3)),serie(R(4),C(2)))
print("z=",iround(z,2))
print("|z|=",str(round(abs(z),2)),
" arg=",str(round(arg(z),2)),"grader")
Studera resultatet: Serie och parallellkopplade resistanser. Klicka på kör.
Låt säga vi inte har några värden på reaktanser (komplexa värden) på komponenterna. Vi har bara det vanliga, resistans, kapacitans och induktans.
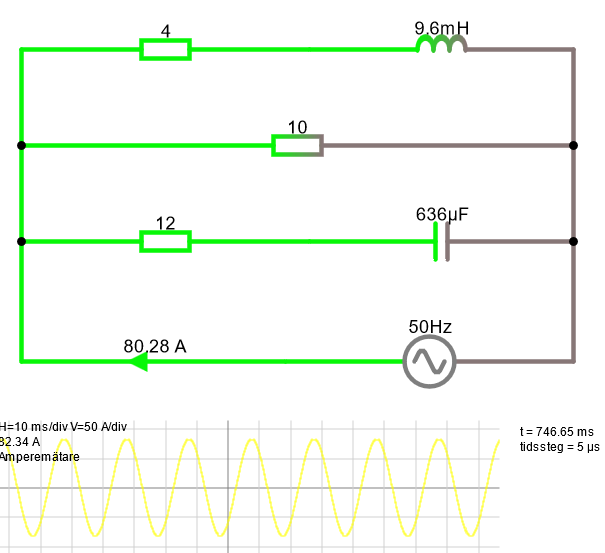
Inga problem! Vi lägger till 2 funktioner och använder formlerna för XL=2πwL och XC=1/(2πwC) och låter python räkna ut reaktanserna. Ja, vi behöver såklart frekvensen men den brukar vara given, i detta fall 50Hz.
import math
def serie(*resistanser):
res = 0
for r in resistanser:
res = res + r
return(res)
def parallell(*resistanser):
res = 0
for r in resistanser:
res = res + 1/r
return(1/res)
def R(r):
return complex(r,0)
def I(z):
return complex(0,z)
def XI(L,f):
return (I(2*math.pi*f*L))
def C(z):
return complex(0,-z)
def XC(F,f):
return (C(1/(2*math.pi*f*F)))
def arg(C):
alfa = math.atan(C.imag/C.real)
return(math.degrees(alfa))
def iround(C,d):
return(complex(round(C.real,d),round(C.imag,d)))
z1 = serie(R(4), XI(0.00955,50))
z2 = R(10)
z3 = serie(R(12),XC(0.000636,50))
zres = parallell(z1,z2,z3)
i = 240/zres
print("i=",iround(i,2))
Studera resultatet: Serie och parallellkopplade resistanser. Klicka på kör.
Stämmer det? Titta i elkrets simulatorn.
Simulatorn är inte alltid exakt. Det beror på att det är svårt att simulera en krets i realtid, i synnerhet om du måste begränsa kalkylen lite pga webbläsarens javascript.
Nu hoppas jag denna sida inspirerat dig att räkna och lära dig python. Lycka till!
OBS Du har alltid tillgång till gratis blixtsnabb python i din mobil eller dator via python-rummet. Behöver inte installera något. Bara tuta och köra.