Jag fick en knasig ide
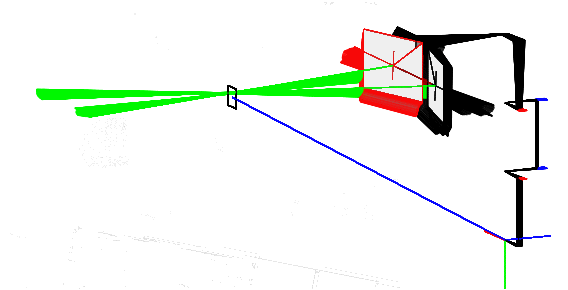
Så jag gjorde en liten skiss
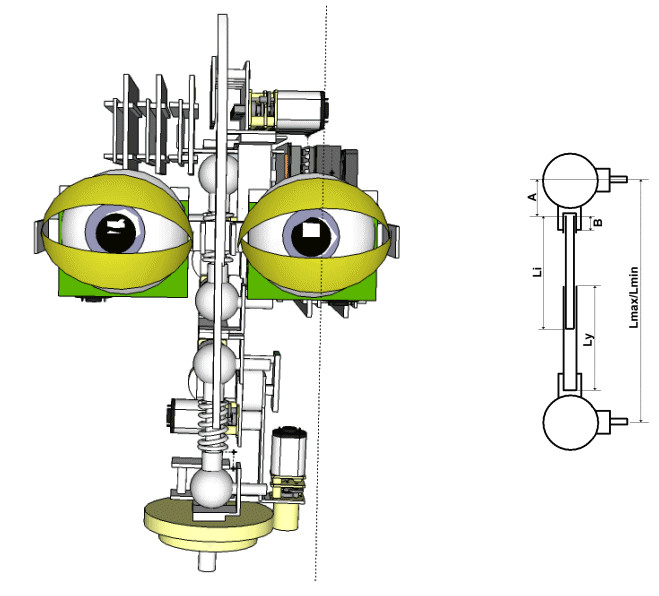
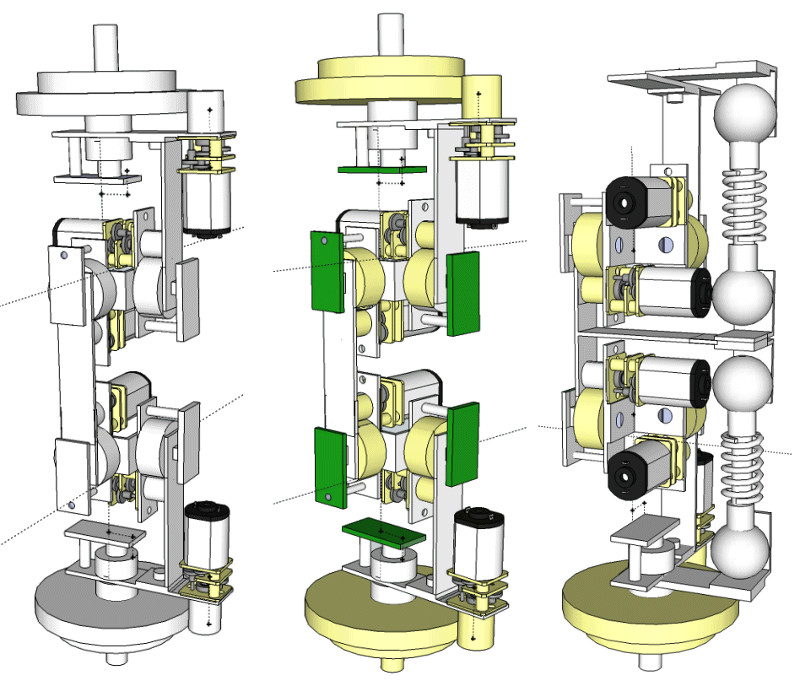
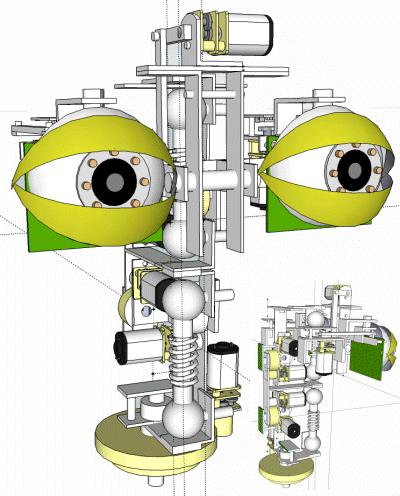
Och började bygga
Byggde ännu mer
Ide'n
Tanken var att huvudet skulle stå där i bokhyllan eller på sängbordet och göra mig lite sällskap. Titta på världen, följa människor med blicken och kanske vara lite spirituell lite då och då.
Så jag hackade ihop en liten lösning för att se om det kunde fungera. För en sådan här grej sitter linjär algebra som handen i handsken.Styrning
Om man har en robot med många leder som rör sig i 3 dimensioner behöver man en vettig matematik i botten för att kunna räkna ut saker och ting, en modell av roboten helt enkelt. Här kommer poängen med linjär algebra in i bilden. Linjär algebra gör det möjligt att knappa in en modell av roboten, robotarmen, robothuvudet eller vad det nu handlar om, i form av begripbara vektorer i ett 3D -rum. En modell vilken man sedan kan snurra och studera lite som man vill. Man kan sedan implementera funktioner för att röra de olika lederna och får både en simulator och kod för robotens rörelser på samma gång.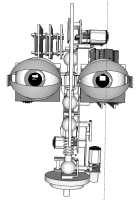
Linjär algebra
Linjär algebra kan man använda för att exempelvis skapa 3D-grafik men det kan också användas för att ge roboten en mer komplett och begriplig modell av sig själv. Det blir sedan enklare att räkna ut servorörelser m.m.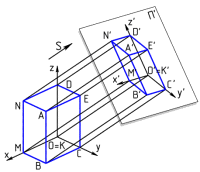
3D Projektion Rotera TransformeringModellen
3D-modellen matas in och lagras i form av punkter (x,y,z). Dessa punkter existerar i en lista och varje punkt har en flagga som berättar om det är en moveto -punkt eller lineto -punkt. Om det är en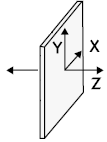
lineto -punkt dras en linje från där senaste linjen slutade eller senaste moveto. Om det är en lineto -punkt kan man även ge den en färg. Eftersom canvas-objektet nu ökar x & y från övre högra hörnet vilket delvis är tväremot vad jag vill har jag inledningsvis roterat trådmodellen så att den hamnar rättvänt i nedre hörnet. X/Y/Z följer alltså tumreglen som det bör göra men trådmodellen är spegelnvänd uppochner i canvas, vilket alltså blir rättvänt.
Rotation och Transformation
När man roterar modellen flyttar man alla modellens punkter. Dvs, vi traverserar alla punkter och flyttar dem enligt de rotationsmatriser vi skapar.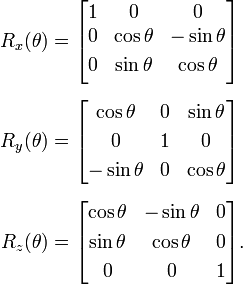
Sedan ritar man om grafiken och drar nya linjer mellan de nya punkterna. Det är ungefär såhär dataspel med 3D-grafik fungerar, fast då brukar man rita polygoner (månghörningar) och sedan fyller man dem med en färg.
För att rotera godtycklig vinkel kring de 3 axlarna skapar vi de tre rotationsmatriserna (bild till höger från wiki) Rx, Ry, Rz. Det ger oss formeln:
Mrot= Morg * Rx * Ry * Rz
Där Morg är vår inknappade modell och Mrot den roterade modellen.
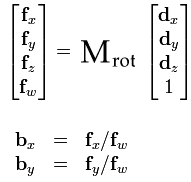För att projicera våra roterade koordinater i 2D -planet (på vår canvas) så multiplicerar vi våra roterade koordinater med en transformationsmatris (se till höger). Vi plockar sedan ut X och Y -koordinaterna ur resultatet (bx, by). Z -koordinaten kan vi också plocka ut för att mäta djupet i bilden för att t.ex. göra linjer framme i bilden tjockare och linjer längre bak tunnare.
Rotatera enbart del av modell
För att rotera enbart en del av 3D-modellen, t.ex. för att vrida på en eller flera leder, finns en funktion som roterar enbart en delmängd av modellens punkter. Man anger ett lägsta och högsta index för modellens punkter så roteras alla punkter i detta intervall. Lite ungefär som om man tänker sig att man formar en bit ståltråd. För att det skall fungera måste man tillfälligt flytta alla punkter i detta intervall till origo kring vilket rotationen sker. Därefter flyttar jag tillbaka de roterade punkterna till den fulla modellen.Skalärprodukt
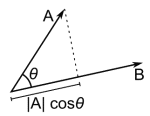Förutom att vrida och vända på hela eller delar av modellen vill jag ibland mäta vinkeln mellan två vektorer för att kunna beräkna något. Det gör man enkelt med skalärprodukten.
Skalärprodukten definieras enligt: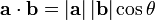
Trådmodell av robot
I detta fall ser alltså modellen ut som nedan. Ögonen fokuserar på föremålet oavsett huvudets läge. Problemet här är att räkna ut rätt vinklar för de servon som styr ögonen. Dvs, vinkeln betraktad ur ögonens servomotorers perspektiv (vinkeln visas avrundad under simulatorn), alltså hur mycket de 3 servomotorer som styr ögonen (höger horisont, vänster horisont samt vertikalled) måste vrida sig givet kroppens position och det som skall fokuseras.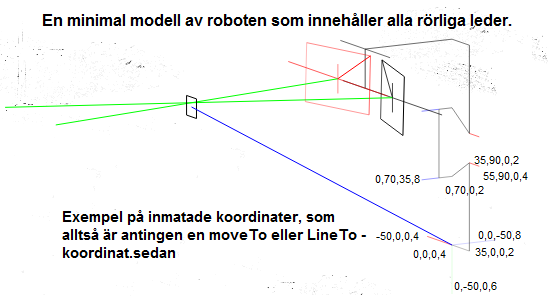
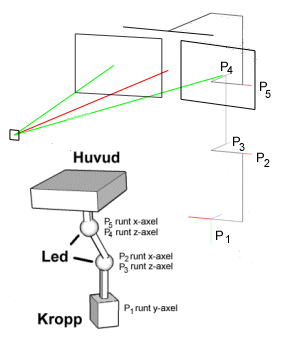Principen för ovanstående skiss är alltså att nacken har 2 rörliga leder och huvudet roterar i botten. Dvs 5 frihetsgrader. På huvudet sitter också 2 ögon med vardera 2 frihetsgrader. Slumpar man en ny fokusvektor kommer ögonen fokusera enligt den.
Variabler
Jag har döpt lederna i nacken till P2 - P5, huvudets rotation är P1.Rumsvektorn, R
För att roboten skall kunna minnas objekt i rummet behövs absoluta vektorer som pekar ut dessa objekt. Dvs, vektorer som är oberoende av hur huvudet rör sig. Jag kallar denna vektor för R.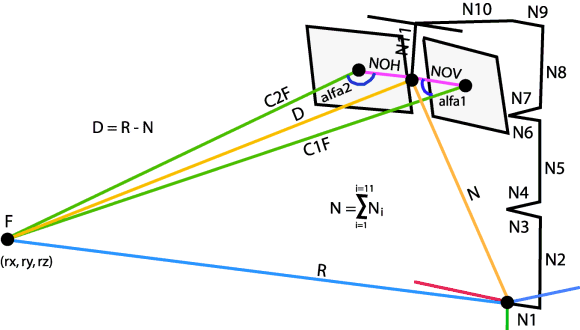
För enkelhetens skull utgår jag härifrån nackens botten eftersom denna position är fixerad (absolut) i rummet. Genom att bilda vektorn R som utgår härifrån kan man enkelt räkna om (uppdatera) D när huvudet rör på sig. D ligger ju sedan till grund för hur ögonen fokuserar objektet ifråga (F i figuren).
Procedur: Allting börjar med R. Jag flyttar sedan lederna i modellen och hämtar N. Jag räknar sedan ut D enligt:
D = R - N
Samt hämtar vektorerna NOH samt NOV. Därefter kan jag räkna ut C1F samt C2F. När jag har dessa kan jag få fram vinklarna för ögonen, vilka roterar kring en vertikalverktor samt horisontalvektor i ögats origo.
Kalkyl vertikalled
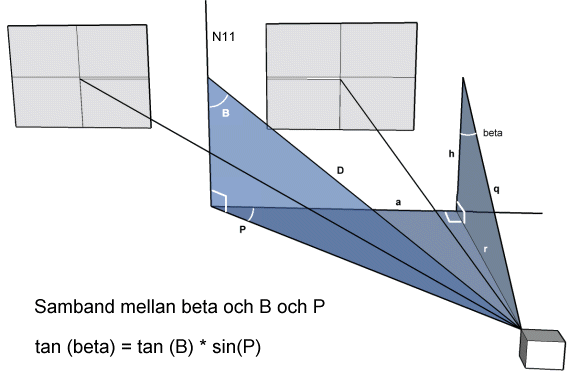
Vinkeln B fås genom att räkna skalärprodukt mellan vektorn D och N11. Den vinkel man får fram fungerar sålänge vinkeln P rör sig kring 90 grader. För att komma runt detta måste man räkna lite till. I själva verket är det vinkeln beta vi vill få fram, som är den mer pålitliga vinkeln ögonen ska röra sig med i vertikalled.
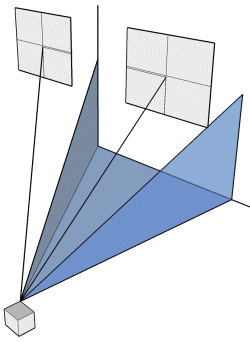
Betraktar man skissen ovan (och till höger) ser man:
(1)
tan (beta) = r / h
(2)
tan (P) = r / a, dvs r = a * tan (P)
(1+2)
tan (beta) = a * tan (P) / h
(3)
a = |D| * sin (B) * cos (P)
(1+2+3)
tan (beta) = |D| * sin (B) * cos (P) * tan (P) / h
tan (beta) = |D| * sin (B) * cos (P) * sin (P) / (h * cos (P))
tan (beta) = |D| * sin (B) * sin (P) / h
(4)
h = |D| * cos (B)
(1+2+3+4)
tan (beta) = |D| * sin (B) * sin (P) / (|D| * cos (B))
tan (beta) = sin (B) * sin (P) / cos (B)
tan (beta) = tan (B) * sin (P)
Dvs, beta = tan-1 (tan (B) * sin (P))
För att testa svaret kan man sätta t.ex. P = 90, dvs ögonen tittar rakt fram.
sin (90) = 1
vilket ger att tan (beta) = tan (B)
vilket ger att beta = B
Vilket ska stämma. Korrigeringen behövs inte vid fokusering av ett föremål precis framför.
Observera rent matematiskt; om B är 90 eller 270 grader finns inget vettigt värde för tangens (B) och datorn kommer ge ifrån sig ett felmedelande. Men för dessa värden behövs ju inte denna funktion som nyss visat så vi kan testa vinkeln B innan vi kör värdet genom funktionen.
Vinklarna för ögonen med de data som ges överst på denna sida beräknas enligt nedan. När ögonens vertikalvinkel räknas ut används vektorn N11. Vinkeln är sedan samma för båda ögon. Alfa räknas ut med ekvationen för skalärprodukten.
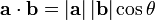
Resultatet: Liten "simulering"
Vrid modellen medsols eller motsols.
Vrid på de olika lederna: +P1 | -P1 | +P2 | -P2 | +P3 | -P3 | +P4 | -P4 | +P5 | -P5
Nollställ | Slumpa ny fokusvektor
Rörelser på tidsaxeln
Så med modellen på plats kan man sedan snickra på rörelser för att få roboten att kännas levande. Då kan man ju fundera lite över vad som egentligen krävs här. Eventuellt kan man åstadkomma rätt så mycket med ganska lite medel.
Operfektionen - ett livstecken
De flesta rörelser vi gör har en poäng, några här nedan är exemplifierade, men det finns även rörelser vi gör utan uppenbar poäng, rent brus. Ungefär som om det "läcker" signaler lite utanför vår tankeprocess som "råkar" sätta kroppen i rörelse. När det är riktigt illa uppfattar vi det kanske som nervositet eller "ticks". Men även om vi är coola gör vi en massa konstiga saker med kroppen utan att det fyller något syfte. Vi kan inte sitta still, vi har händerna i ansiktet, känner på läpparna, kliar oss på armarna, flyttar omkring fötterna, gör en massa underliga saker med tungan och munnen, vrider oss på stolen för att hitta en mer bekväm ställning. osv.Dessa nervösa och fysiologiska brister har inte en robot. Den rör sig inte en mikrometer utan någon anledning. Den är stilla som urberget. Problemet är bara att vi människor är så vana vid att detta brus är en del av livet att när bruset uteblir uppfattar vi någonting som dött.
Om man köper att det är på detta vis och vill arbeta för att människor ska ta till sig en robot, då är det viktigt att roboten åtminståne imiterar detta beteende. Spännande är iofs om man kan låta robotens tänkande "läcka" lite eftersom man då samtidigt får viss feedback vad roboten tänker på. Oavsett vilket handlar det alltså om att roboten ibland rör lite på nacken och huvudet, flyttar blicken ett kort ögonblick som om något distraherade maskinen, osv.
Blinka med ögonen
Forskning på robot-människa -interaktion har visat att en mycket viktig detalj för att roboten skall kännas närvarande är den att roboten blinkar med ögonen. Det kanske inte är så märkvärdigt egentligen. Det är ju faktiskt något vi människor gör kontinuerligt för att våra ögonen skall hållas fuktiga och rena och som vi troligtvis gjort till en undermedveten signal för att känna igen levande väsen.Ändra blickriktning
Det är viktigt även hur ögon och huvud rör sig. Då ögonen är små och lättrörliga ligger det nära till hands att först och främst flytta blickriktningen med ögonen. Det går snabbt och lätt. Om vi flyttar blicken med ögonen annat än högst tillfälligt, så riktar vi om hela huvudet - med hjälp av nacken - i den riktning vi vill titta. De lättrörliga snabba ögonen kommer först och därefter släpar det tyngre lite trögrörligare huvudet efter. Om vi står väldigt länge och tittar kommer vi antagligen sedan också vända hela vår kropp mot det vi tittar på. Min robot har ingen kropp, så sistnämda är inte aktuellt.Kroppsspråk (ögon - nacke)
Tänkande, Uttråkad
När vi tänker så tittar vi ibland upp, ungefär som om vi skapade bilder i huvudet som vi måste lyfta ögonen för att kunna se. Tänkande kan ibland inkludera att vi är uttråkade och känner en hopplösthet och att vi då tittar upp för att slippa se det vi har framför oss.Uttråkad, Uppgivenhet
Om vi känner sorg eller uppgivenhet tittar vi istället ner i backen och kan ibland även låta nacken "falla ihop" när vi tittar ner ungefär som om all kraft tagit slut.Ifrågasättande
Huvud böjt framåt men bibehållen ögonkontakt kan indikera ett ifrågasättande.Mallighet, makt, dominans (huvuv böjt bak)
Huvud böjt bakåt men bibehållen ögonkontakt signalerar domanians.Förvåning, Överaskning
När vi är förvånade öppnar vi våra fokuserade ögon skjuter nacken bakåt ungefär som om vi för att vara säkra ville skydda oss från det vi upptäckt.Nyfikenhet
När vi är nyfikna fokuserar vi med öppna ögon det vi är nyfikna på och skjuter fram nacken för att komma närmare och tydligare se det vi vill se.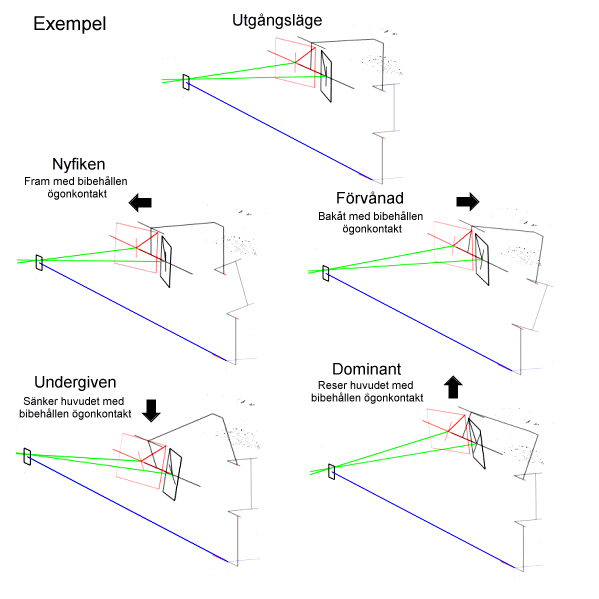
Kod
Koden skriven i javascript nedan. Dels kod för matris-operationer och dels huvudprogrammet. Koden skrevs för att det skulle vara enkelt koda om till C och stoppa in i en simpel processor. Observera att nedan är tänkt styra servorn. Det behövs naturligtvis något som fångar upp vad roboten ser också. Detta kan göras t.ex. med en raspberry PI i vilken man installerar opencv. Med Opencv är det en barnlek identifiera ansikten eller andra föremål. Jag ska skriva något om opencv en annan dag.
// http://el.st/
//
// Om du gillar el.st - sätt en länk!
//
var max = new Array(320); // 20 st
var vi = new Array(300);
var vo = new Array(300);
var vcnt=0;
var stls = new Array('','','0,0,0','','255,0,0','','0,255,0','','0,0,255');
function getv_x(a)
{
return(vi[a+1]);
}
function getv_y(a)
{
return(vi[a+2]);
}
function getv_z(a)
{
return(vi[a+3]);
}
function eget(n,x,y)
{
return(max[n*16+x+y*4]);
}
function eset(n,x,y,v)
{
max[n*16+x+y*4]=v;
}
function assign(a,b)
{
var x, y;
for (x=0;x<4;++x)
for (y=0;y<4;++y)
eset(a,x,y,eget(b,x,y));
}
function umatrix(n)
{
var x, y;
for (x=0;x<4;++x)
for (y=0;y<4;++y)
eset(n,x,y,(x==y)?1:0);
}
// multplicera a med b, svaret i c, w bredd på matris
function mult(a,b,c,w)
{
var x,y,z,s;
for (x=0;x<w;++x)
for (y=0;y<4;++y)
{
for (s=0,z=0;z<4;++z)
s+=eget(a,z,y)*eget(b,x,z);
eset(c,x,y,s);
}
}
function rotate( x, y, z ) // skapa rotationsmatris i
{
umatrix(5);
eset(5,1,1,Math.cos(x));
eset(5,2,2,Math.cos(x));
eset(5,1,2,Math.sin(x));
eset(5,2,1,-Math.sin(x));
umatrix(6);
eset(6,0,0,Math.cos(y));
eset(6,2,0,Math.sin(y));
eset(6,0,2,-Math.sin(y));
eset(6,2,2,Math.cos(y));
// q(7)= r(5) * g(6)
mult(5,6,7,4);
umatrix(6);
eset(6,0,0,Math.cos(z));
eset(6,1,1,Math.cos(z));
eset(6,0,1,Math.sin(z));
eset(6,1,0,-Math.sin(z));
// r = q * g
mult(7,6,5,4);
// q = r * this
mult(5,0,3,4);
assign(0,3);
}
function pos( x, y, z )
{
umatrix(8);
eset(8,3,0,x);
eset(8,3,1,y);
eset(8,3,2,z);
assign(9,0);
mult(8,9,10,4);
assign(0,10);
}
function mTo(x,y,z)
{
vi[vcnt]=1;
vi[vcnt+1]=x;
vi[vcnt+2]=y;
vi[vcnt+3]=z;
vcnt+=4;
}
function lTo(x,y,z,c)
{
vi[vcnt]=c;
vi[vcnt+1]=x;
vi[vcnt+2]=y;
vi[vcnt+3]=z;
vcnt+=4;
}
function transform()
{
var i=0,w;
while (i<vcnt)
{
eset(1,0,0,vi[i+1]);
eset(1,0,1,vi[i+2]);
eset(1,0,2,vi[i+3]);
eset(1,0,3,1);
mult(0,1,2,1); // 1 bred
w=eget(2,0,3);
vo[i]=vi[i];
vo[i+1]=eget(2,0,0)/w;
vo[i+2]=eget(2,0,1)/w;
vo[i+3]=eget(2,0,2)/w;
i+=4;
}
}
function pretransform(s,e) // start
{
var i=0,w,x=0,y=0,z=0;
if(s>0)
{
x=vi[s+1];
y=vi[s+2];
z=vi[s+3];
i=s;
}
i=((e==0)?vcnt:e);
while (i>=s)
{
eset(1,0,0,vi[i+1]-x);
eset(1,0,1,vi[i+2]-y);
eset(1,0,2,vi[i+3]-z);
eset(1,0,3,1);
mult(0,1,2,1); // 1 bred
w=eget(2,0,3);
vi[i]=vi[i];
vi[i+1]=x+eget(2,0,0);
vi[i+2]=y+eget(2,0,1);
vi[i+3]=z+eget(2,0,2);
i-=4;
}
}
function prerotate( x, y, z, s, e ) // skapa rotationsmatris i
{
rotate( x, y, z );
pretransform(s,e);
}
function drawVect(bl)
{
var i=0,tz=0,z2;
while (i<vcnt)
{
z2=(400-vo[i+3]-tz)/400;
// z2=255;
ctx.strokeStyle = 'rgba('+stls[vo[i]]+','+z2+')';
if(!(vo[i]%2))
{
ctx.beginPath();
if((bl==1)&&((i==176)||(i==208)))
{
ctx.strokeStyle = 'rgba('+'240,240,240'+','+z2+')';
ctx.fillStyle = 'rgba('+'128,128,128'+','+z2+')';
ctx.moveTo(vo[i+1-4],vo[i+2-4]);
ctx.lineTo(vo[i+1],vo[i+2]); i+=4;
ctx.lineTo(vo[i+1],vo[i+2]); i+=4;
ctx.lineTo(vo[i+1],vo[i+2]); i+=4;
ctx.lineTo(vo[i+1],vo[i+2]); i+=4;
ctx.lineTo(vo[i+1],vo[i+2]);
ctx.fill();
}
else
{
ctx.moveTo(vo[i+1-4],vo[i+2-4]);
ctx.lineTo(vo[i+1],vo[i+2]);
tz=vo[i+3];
ctx.stroke();
}
}
i+=4;
}
}
Koden för att få denna vektor -snubbe att leva enligt nedan. Observera att detta är ett spontant experiment och koden är därför "ett hack". En robot i serieproduktion som ska rädda livet på människor behöver en mer solid verifierbar kod.
// http://el.st/
//
// Om du gillar el.st - sätt en länk!
//
var v=-0.1,dir=1;
var bgimg=new Image(500,400);
bgimg.src="canvasback.gif";
var hPI=Math.PI/2;
var rx=0; // höger-vänster från huvudet, vänster positivt värde
var ry=171; // upp-ner, lägre värde längre ner, 170 rakt fram
var rz=300; // avstånd
var ox=nx=0,oy=ny=0,oz=nz=0;
var le_alfa=0;
var re_alfa=0;
var l_beta=0;
var info="", info_vinklar="";
var p1=0,p2=0,p3=0,p4=0,p5=0;
var d_vinkel;
var re_blk=0;
var re_blkwait=20;
var re_blktime=4;
var p5_bias1=0;
var p5_bias1dir=0;
var p5_bias2=0;
var p1_bias1=0;
var p1_bias1dir=0;
var em_tkr1=0;
var em_tkr2=0;
var et_tst=-1; // "se söt ut"
var et_und=-1; // undergiven
var et_dom=-1; // dominans
var et_sca=-1; // rädd
var et_cur=-1; // nyfiken
var et_att=-1; // attityd
var et_dir=0; // --"-- riktning
var et_him=-1; // himla med ögonen
var ry_old;
function setText(id,txt)
{
document.getElementById(id).innerHTML=txt;
}
window.onload = function()
{
ctx = document.getElementById('c').getContext('2d');
setup_vectors();
calc();
redraw();
setInterval( 'focus_head()', 100 );
}
function left_eye(beta,alfa)
{
umatrix(0);
prerotate(beta-Math.PI/2,3*Math.PI/2-alfa,0,172,200);
}
function right_eye(beta,alfa)
{
umatrix(0);
prerotate(beta-Math.PI/2,Math.PI/2-alfa,0,204,232);
}
function objekt()
{
mTo(rx-10,ry+10,rz,2);
lTo(rx+10,ry+10,rz,2);
lTo(rx+10,ry-10,rz,2);
lTo(rx-10,ry-10,rz,2);
lTo(rx-10,ry+10,rz,2);
}
function setup_vectors()
{
vcnt=0;
// objekt
mTo( 0,0,0,4 );
lTo( -50,0,0,4 ); // R
mTo( 0,0,0,4 );
lTo( 0,-50,0,6 ); // G
mTo( 0,0,0,4 );
lTo( 0,0,-50,8 ); // B
// robot
mTo(0,0,0,2 );
lTo(35,0,0,2 ); // 35
lTo(35,70,0,2 ); // 70 mm upp
// röd p1
mTo( 35,70,0,4 );
lTo( 45,70,0,4 );
mTo(35,70,0,2);
lTo(0,70,0,2 ); //
lTo(0,70,-35,2 ); //
// blå p2
mTo( 0,70,-35,4 );
lTo( 0,70,-45,8 );
mTo(0,70,-35,2);
lTo(0,140,-35,2 ); //
// blå p3
mTo( 0,140,-35,4 );
lTo( 0,140,-45,8 );
mTo(0,140,-35,2 );
lTo(0,140,0,2 ); //
lTo(35,140,0,2 ); //
// röd p4
mTo( 35,140,0,4 );
lTo( 45,140,0,4 );
mTo(35,140,0,2 );
lTo(35,210,0,2 ); //
lTo(0,210,0,2 ); // ---
lTo(0,210,0,2 ); // sista nacken
lTo(0,210,100,2 ); // huvud till ögon
lTo(0,170,100,2 ); // N11
mTo(50,210,100,2 ); // från vänster till ..
lTo(-50,210,100,2 ); // höger öga
mTo(0,210-40,100,2 ); // fokusvektor
mTo(rx,ry,rz,4 ); // osynliggör genom en dummymove
mTo(55,210-35-20,100,2 ); // vänster vertikalvektor
lTo(55,210-45+20,100,2 );
mTo(55+100,210-40,100,2 ); // vänster horisontalvektor
lTo(55-100,210-40,100,2 );
mTo(-55,210-35-20,100,2 ); // höger vertikalvektor
lTo(-55,210-45+20,100,4 );
mTo(-55-100,210-40,100,2 ); // höger horisontalvektor
lTo(-55+100,210-40,100,4 );
mTo(55,170,100,2 ); // P0
lTo(10,200,100,2 ); // P1
lTo(10,140,100,2 ); // P2
lTo(100,140,100,2 ); // P3
lTo(100,200,100,2 ); // P4
lTo(10,200,100,2 ); // -> P1
mTo(55,210-40,100,2 ); // vänster fokusvektor
lTo(55,210-40,500,6 );
mTo( -55,170,100,4 );
lTo( -10,200,100,4 );
lTo( -10,140,100,4 );
lTo(-100,140,100,4 );
lTo(-100,200,100,4 );
lTo( -10,200,100,4 );
mTo(-55,210-40,100,2 ); // vänster fokusvektor
lTo(-55,210-40,500,6 );
objekt();
mTo( 0,0,0,4 );
lTo( rx,ry,rz,8 );
}
function vert_comp(B,P)
{
if ((B==(Math.PI/2))||(B==(3*Math.PI/2)))
{
return B;
}
else
{
if(B<(Math.PI/2))
return Math.PI+Math.atan(Math.tan(B) * Math.sin(P));
else
return Math.atan(Math.tan(B) * Math.sin(P));
}
}
function calc()
{
var subtot, vx,vy,vz,lx,ly,lz,rrx,rry,rrz,nox,noy,noz,v2x,v2y,v2z,dvx,dvy,dvz,L,Z,N11nx,N11nz,N11ny,N11xz_abs,i,j,k;
var N10x, N10y, N10z,N10_sum;
// N-vektorn + N11
nx=getv_x(120);
ny=getv_y(120);
nz=getv_z(120);
// D-vektorn
ox=rx-nx;
oy=ry-ny;
oz=rz-nz;
var alfa_v,alfa_h,beta;
x=ox;
y=oy;//-210+40;
z=oz;//-100;
nox=nx-getv_x(204);
noy=ny-getv_y(204);
noz=nz-getv_z(204);
// rött öga
// höger öga
C2Fx=x+nox;
C2Fy=y+noy;
C2Fz=z+noz;
xyz=C2Fx*C2Fx+C2Fy*C2Fy+C2Fz*C2Fz;
subtot_t=nox*C2Fx+noy*C2Fy+noz*C2Fz;
var hxyz_abs=Math.sqrt(nox*nox+noy*noy+noz*noz);
alfa_v=subtot_t/(Math.sqrt(xyz)*hxyz_abs);
alfa_v= Math.acos(alfa_v);
re_alfa=alfa_v; // justera höger öga
alfa_v=Math.round(365/2/Math.PI*alfa_v);
// info_vinklar='Servorörelser ögon: Vänster = '+alfa_v+' grader ';
// svart öga
// vänster öga
nox=nx-getv_x(172);
noy=ny-getv_y(172);
noz=nz-getv_z(172);
C1Fx=x+nox;
C1Fy=y+noy;
C1Fz=z+noz;
xyz=C1Fx*C1Fx+C1Fy*C1Fy+C1Fz*C1Fz;
subtot_t=nox*C1Fx+noy*C1Fy+noz*C1Fz;
var hxyz_abs=Math.sqrt(nox*nox+noy*noy+noz*noz);
alfa_h=subtot_t/(Math.sqrt(xyz)*hxyz_abs);
alfa_h= Math.acos(alfa_h);
le_alfa=-alfa_h; // justera höger öga
alfa_h=Math.round(365/2/Math.PI*alfa_h);
// info_vinklar=info_vinklar+' | Höger = '+alfa_h+' grader ';
// C1F samma
// 1. Sätt vektorn v = vektorn N11
vx=getv_x(120)-getv_x(116);
vy=getv_y(120)-getv_y(116);
vz=getv_z(120)-getv_z(116);
d_vinkel=(alfa_v-alfa_h)/2+90;
d_vinkel=d_vinkel/180*Math.PI;
// 2. Fixa ekvationerna
subtot_t=vx*ox+vy*oy+vz*oz;
vxyz_abs=Math.sqrt(vx*vx+vy*vy+vz*vz);
var beta=subtot_t/(Math.sqrt(xyz)*vxyz_abs);
beta= Math.acos(beta);
beta=365/2/Math.PI*beta;
beta=vert_comp(beta/180*Math.PI,d_vinkel);
l_beta=2*Math.PI-beta;
if(l_beta>(Math.PI*2))
l_beta-=Math.PI*2;
info_vinklar=info_vinklar+' | Vertikalt = '+Math.round(l_beta*180/Math.PI)+' grader</u><br/>';
// setText("data2",info);
// setText("data1",info_vinklar);//info_vinklar);
}
function focus_head()
{
var adj=-1;
var fh1=(l_beta-(Math.PI/2));
var fh2=((Math.PI/2)-d_vinkel);
if(et_him>0)
{
fh1=0;
fh2=0;
p5_bias1=0;
}
if(l_beta>(Math.PI/2))
{
adj=0;
move_p5(fh1/4+p5_bias1+p5_bias2); // addera för blyg bort för dominant
}
if(l_beta<(Math.PI/2))
{
adj=0;
move_p5(fh1/4+p5_bias1+p5_bias2); // addera för blyg bort för dominant
}
if(d_vinkel>(Math.PI/2))
{
adj=0;
move_p1(fh2/4+p1_bias1);
}
if(d_vinkel<(Math.PI/2))
{
adj=0;
move_p1(fh2/4+p1_bias1);
}
if((et_und+et_dom+et_sca+et_cur+et_att+et_att+adj)==-7)
{
p1=0;
p2=0;
p3=0;
p4=0;
p5=0;
}
redraw();
}
function newfocus()
{
rx=Math.round(Math.random()*200)-100; 0; // höger-vänster från huvudet, vänster positivt värde
ry=Math.round(Math.random()*100)+100; // upp-ner, lägre värde längre ner, 170 rakt fram
rz=Math.round(Math.random()*350)+200; // avstånd
redraw();
}
function scare()
{
p2=0;
et_sca=1;
et_cur=-1;
}
function cur()
{
p2=0;
et_cur=1;
et_sca=-1;
}
function twist()
{
p4=0;
et_tst=1;
et_dir=(Math.random()>=0.5)?1:-1;
}
function domin()
{
p5_bias2=0;
et_dom=1;
et_und=-1;
}
function blyg()
{
p5_bias2=0;
et_dom=-1;
et_und=1;
}
function attityd()
{
p3=0;
p4=0;
et_att=1;
et_dir=(Math.random()>=0.5)?1:-1;
}
function himla()
{
if(et_him<0)
{
ry_old=ry;
}
et_him=1;
}
function redraw()
{
if(window.innerWidth<600)
{
ctx.canvas.width = window.innerWidth-100;
}
else
{
ctx.canvas.width = 500;
}
setup_vectors();
// p2 (x)
umatrix(0);
prerotate(p2,0,0,36,232);
// p3 (z)
umatrix(0);
prerotate(0,0,p3,52,232);
// p4 (z)
umatrix(0);
prerotate(0,0,p4,72,232);
// p5 (x)
umatrix(0);
prerotate(p5,0,0,88,232);
// p1 (y)
umatrix(0);
prerotate(0,p1,0,24,232);
calc();
// gör om i rätt ordning
setup_vectors();
right_eye(l_beta,re_alfa);
left_eye(l_beta,le_alfa);
// p2 (x)
umatrix(0);
prerotate(p2,0,0,36,232);
// p3 (z)
umatrix(0);
prerotate(0,0,p3,52,232);
// p4 (z)
umatrix(0);
prerotate(0,0,p4,72,232);
// p5 (x)
umatrix(0);
prerotate(p5,0,0,88,232);
// p1 (y)
umatrix(0);
prerotate(0,p1,0,24,232);
umatrix(0);
rotate(Math.PI+0.2,Math.PI+v+2.3,0);
pos(c.width-40,250,150);
transform();
em_tkr1++;
em_tkr2++;
if(re_blk--<-re_blkwait)
{
re_blk=re_blktime;
re_blktime=1;
re_blkwait=Math.round(Math.random()*15)+10;
}
if((em_tkr1>180)&&(em_tkr1<270))
{
if(em_tkr1==181)
{
p1_bias1dir=Math.random()>0.5?1:-1;
}
p1_bias1=(Math.cos(em_tkr1*10/360*(Math.PI/2))-0.3)/40*p1_bias1dir;
}
if(em_tkr1>300)
{
em_tkr1=0;
}
if((em_tkr2>180)&&(em_tkr2<270))
{
if(em_tkr2==181)
{
p5_bias1dir=Math.random()>0.5?1:-1;
}
p5_bias1=(Math.cos(em_tkr2*10/360*(Math.PI/2))-0.3)/40*p5_bias1dir;
}
if(em_tkr2>280)
{
em_tkr2=0;
}
if(et_tst>0)
{
et_tst++;
if(et_tst<20)
{
p4+=0.01*et_dir;
}
if(et_tst>40)
{
p4-=0.01*et_dir;
}
if(et_tst>55)
{
et_tst=-1;
}
}
if(et_sca>0)
{
et_sca++;
if(et_sca<9)
{
re_blk=1;
p2-=0.05;
}
if(et_sca>=9)
{
p2+=0.0025;
}
if(et_sca>126)
{
et_sca=-1;
}
}
if(et_cur>0)
{
et_cur++;
if(et_cur<30)
{
p2+=0.01;
}
if(et_cur>=50)
{
p2-=0.01;
}
if(et_cur>75)
{
et_cur=-1;
}
}
if(et_dom>0)
{
et_dom++;
if(et_dom<10)
{
p5_bias2-=0.017;
}
if(et_dom>=50)
{
p5_bias2+=0.017;
}
if(et_dom>56)
{
et_dom=-1;
}
}
if(et_und>0)
{
et_und++;
if(et_und<10)
{
p5_bias2+=0.017;
}
if(et_und>=50)
{
p5_bias2-=0.017;
}
if(et_und>56)
{
et_und=-1;
}
}
if(et_att>0)
{
et_att++;
if(et_att<10)
{
p3+=0.04*et_dir;
p4-=0.04*et_dir;
}
if((et_att>10)&&(et_att<30))
{
p3-=0.04*et_dir;
p4+=0.04*et_dir;
}
if(et_att>30)
{
p3+=0.04*et_dir;
p4-=0.04*et_dir;
}
if(et_att>40)
{
et_att=-1;
}
}
if(et_him>0)
{
et_him++;
if(et_him<8)
{
re_blk=1;
ry+=20;
}
if((et_him>28)&&(et_him<31))
{
re_blk=0;
ry-=20;
}
if(et_him>32)
{
ry=ry_old;
}
if(et_him>33)
{
et_him=-1;
}
}
p1+=(Math.random()-1)/800;
p5+=(Math.random()-1)/400;
ctx.drawImage(bgimg,0,0);
drawVect(re_blk>0?1:0);
}
function move_p1(off)
{
p1+=off;
redraw();
}
function move_p2(off)
{
p2+=off;
redraw();
}
function move_p3(off)
{
p3+=off;
redraw();
}
function move_p4(off)
{
p4+=off;
redraw();
}
function move_p5(off)
{
p5+=off;
redraw();
}
function vect_rst()
{
p1=0;
p2=0;
p3=0;
p4=0;
p5=0;
redraw();
}
function rotate_mod(off)
{
v+=off;
redraw();
}
Lite funderingar
Om du exprimenterar med ovanstående modell så ser du att roboten inte riktigt lyckas fokusera från stora horisontalvinklar betraktat ut huvudets/nackens perspektiv, ifall den vrider på huvudet vänster/höger samtidigt. Jag tror det har att göra med att vertikalvinkeln räknas från en tänkt punkt mellan ögonen. Nu spelar detta ingen som helst roll. Människor lyckas inte med detta konststycke heller och jag orkar inte fixa det nu oavsett.Ovan ska mest uppfattas som inspiration. Du kan göra något bättre än vad jag hackat ihop här. Jag ska grotta djupare i detta en annan dag.
Lycka till!
PS. Jag har börjat snickra på en ny ide. Såhär är ögonen gjorda.
