Sekvensnät
Vad måste man fatta för att begripa hur sekvensnät fungerar?Klockade vippor, Q och Q+
Klocksignal ...
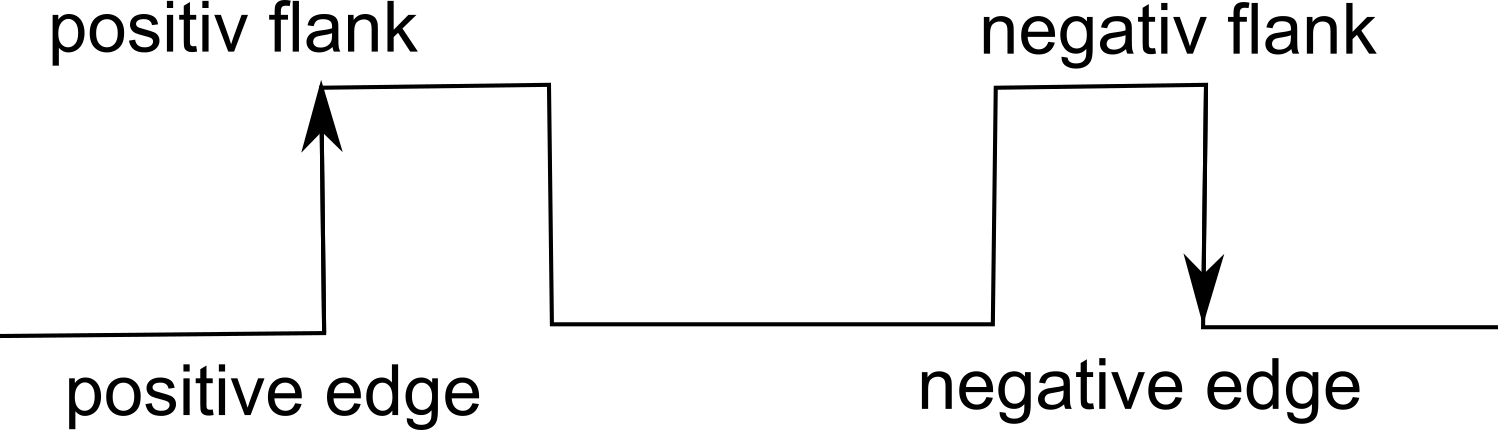
Vippor med ingång för en klocksignal är vippor som endast ändrar tillstånd när det kommer en klocksignal. Själva ändringen sker antingen på positiv eller negativ flank, dvs i det ögonblick då vi har en positiv eller negativ flank. Nedan pratar jag enbart om klockpuls, "vid klockpuls". Det är underförstått att omslaget sker vid den positiva eller negativa flanken.
Q+ avser värde efter klockpulsen, dvs det som vippan ändrar värde till. Värdet ändras från Q till Q+.
Alla dessa vippor har 2 utgångar, både Q och inversen av Q. Det visar sig att detta är mycket användbart när man kopplar ihop flera vippor och även behöver den inverterade utgången. Det är därför den finns där.
De olika vipporna
D-vippa
D som i data. Ingången på en d-vippa är en "dataingång". Vid varje klockpuls sätts utgången Q till värdet på ingången.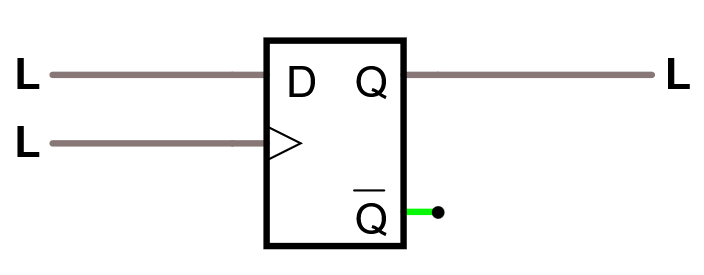
Vid varje klockpuls kommer Q bli vad D är, dvs Q = D vid varje klockpuls. Om D ändras mellan klockpulserna spelar ingen roll. Det är vad D är precis i det ögonblick då klockpulsen har en positiv (eller negativ, beror på krets) flank som bestämmer vad Q blir.
| D | Q |
| 0 | 0 |
| 1 | 1 |
Exprimentera med D-vippa i simulatorn.
T-vippa
T som i engelska ordet toggle, dvs växla eller flippa. Det är vad T -vippan gör, flippar utgången om T = 1.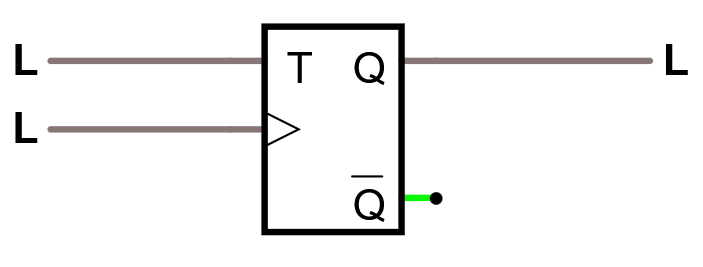
Vid varje klockpuls händer något eller inget. Om T = 0, så händer inget, dvs om Q = 0 innan så är Q = 0 efter. Om T = 1, så flippas (inverteras) utgången. Vi kan kalla T = 1 för flipp -mode. Är T = 1 så inverteras/flippas alltid utgången.
| T | Q | Q+ |
| 0 | Q | Q |
| 1 | Q | Q |
Exprimentera med T-vippa i simulatorn.
JK-vippa
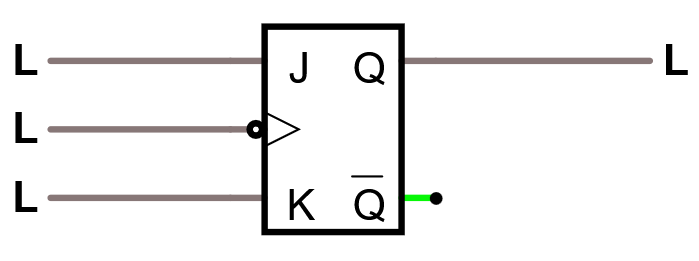
En JK -vippa fungerar som en SR -vippa, fast där SR -vippan har ett förbjudet tillstånd S=R=1, där har JK -vippan istället en feature, nämligen att J=K=1 flippar utgången.
| J (set) | K (reset) | Q | Q+ |
| 0 | 0 | Q | Q |
| 1 | 0 | Q | 1 |
| 0 | 1 | Q | 0 |
| 1 | 1 | Q | Q |
Exprimentera med JK -vippa i simulatorn.
Tillståndsmaskin
Synkron
En tillståndsmaskin är en krets som vid varje triggsignal övergår till nytt tillstånd, under påverkan av dels tidigare tillstånd samt ev yttre signaler.Autonoma och icke autonoma
Ett autonomt sekvensnät är helt enkelt en tillståndsmaskin som räknar vid varje klockpuls och inte reagerar på något annat. Detta till skillnad från en tillståndsmaskin som även reagerar på andra signaler, t.ex. en klocksignal och en insignal från en knapp. De fungerar likadant förutom att de kombinatoriska nät som styr insignalerna i sistnämnda fall också tar hänsyn till andra insignaler.Konstruktion
En tillståndsmaskin kan bestå av ett antal vippor (SR, D, JK eller T). 2 vippor kan hantera 4 tillstånd. 3 vippor kan hantera 8 tillstånd osv.Till skillnad från en vanlig räknare som bara räknar upp (t.ex. 000, 001, 010, 011. 100, 101, 110, 111, ...) så kan en tillståndsmaskin räkna i vilken ordning som helst. Det är ditt projekt att se till att den räknar som du vill. Så hur kan vi styra hur den räknar? Vi kanske vill ha en sekvens såhär 00, 11, 10, 01, 00, ...
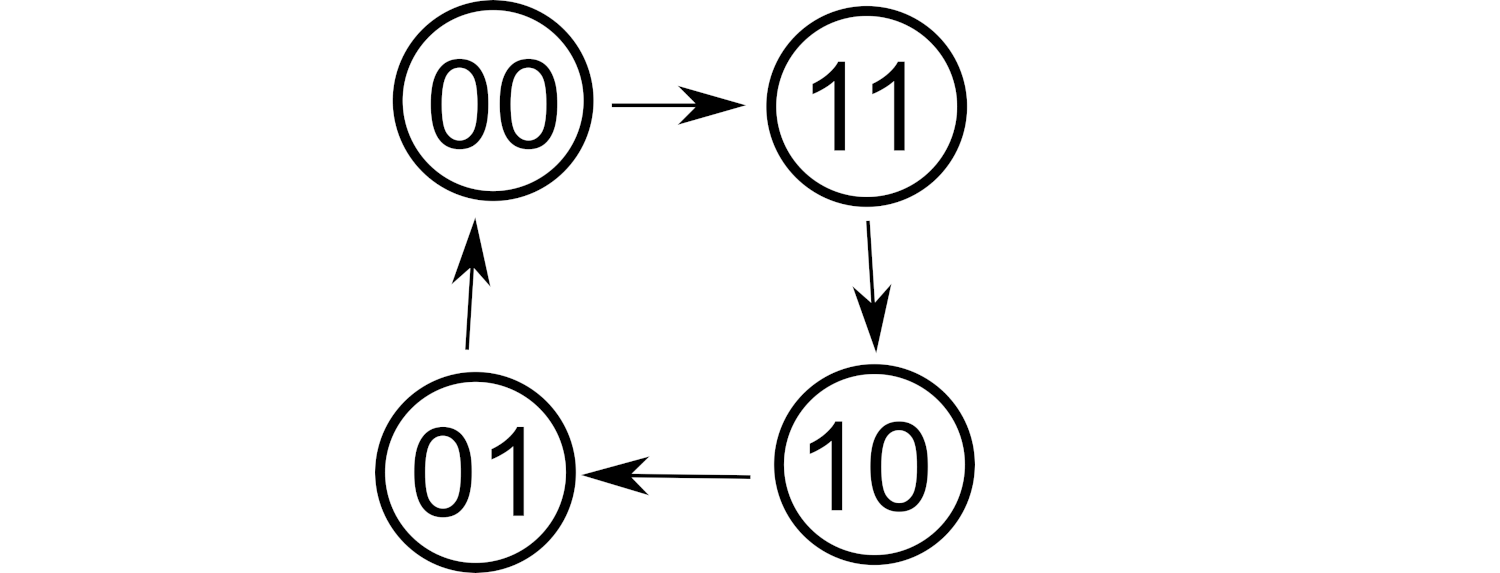
Vi börjar med att göra en tabell där vi tänker oss att vi räknar upp alla kombinationer av 2 vippor.
| Q1 | Q0 |
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
Därefter återgår vi till att titta noga på vår sekvens som vi ville skapa, nämligen: 00, 11, 10, 01. Studera sekvensen noga. Efter tillståndet 00, vad kommer då? Efter 11, vad kommer då? Efter 10, vad kommer då? Efter 01, vad kommer då när sekvensen börjar om? Ta det långsamt steg för steg och gör en tabell med tillstånden Q+ som följer efter Q.
| Q1 | Q0 | Q1+ | Q0+ |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
När du gjort tabellen tar du fram suddigummi och gör om allting eftersom du glömde göra plats för lite fler kolumner, nämligen ingångarna på D-vipporna.
D -vippor
Det är vippornas ingångar (D i detta fall) vi måste fixa logik till. Beroende på vad Q0 och Q1 är, så skall ingångarna på vipporna vara ditten eller datten.
| Q1 | Q0 | D1 | Q1+ | D0 | Q0+ |
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 1 | 1 | 0 |
Häng med nu! Titta ovan. Om Q0=0 och Q1 = 0, så vill vi att utsignalen från Q1+ = 1. Vad måste då insignalen till vippa 1 vara, för att utsignalen skall vara 1 ?. Vi kan ställa oss frågan för alla signaler. Det blir väl som nedan, eller hur? D -vippan fungerar ju så, att insignalen blir utsignal vid nästa klockpuls?
| Q1 | Q0 | D1 | Q1+ | D0 | Q0+ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Så, vad måste isåfall Q0 och Q1 vara för att D0 respektive D1 ska få sina värden efter nästa klockpuls? Vi kan titta på det som ett kombinatoriskt nät, där Q0 och Q1 är insignaler och D0 och D1 utsignaler. Är det enkelt, kan vi skriva ner algebran direkt. Är det svårt, gör vi t.ex. karnaugdiagram.
D1 = Q0 Q1 + Q0 Q1 samt D0 = Q0
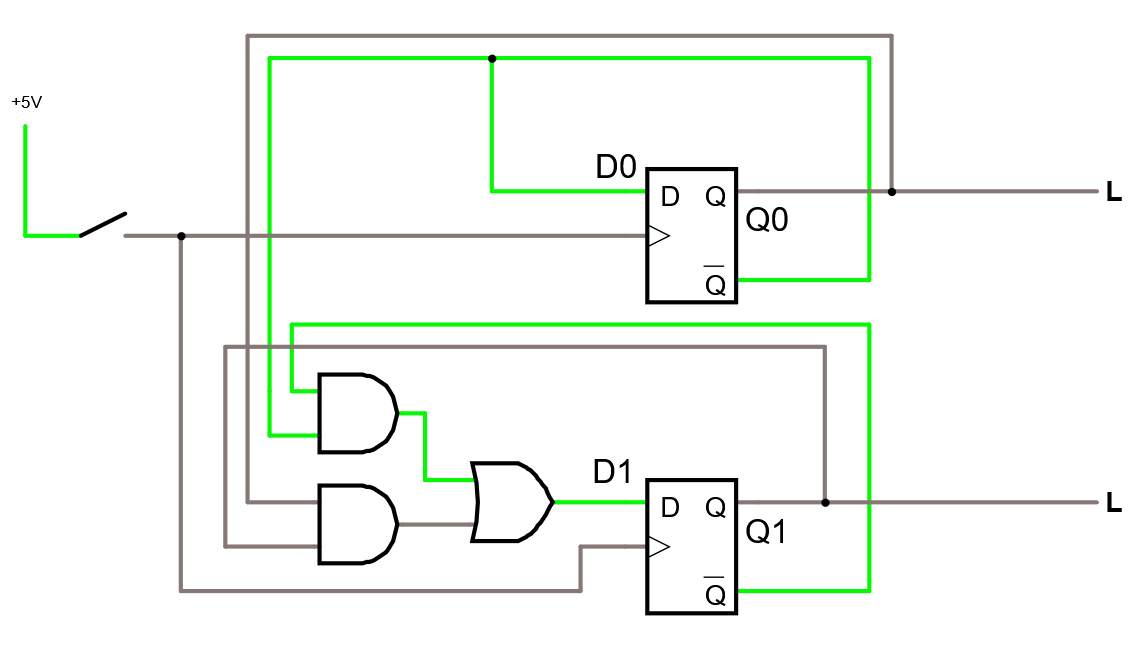
Studera funktionen i krets-simulatorn.
Eftersom logiken är uppbyggd med AND och OR, så kan vi lätt konvertera till NAND om det är önskvärt.
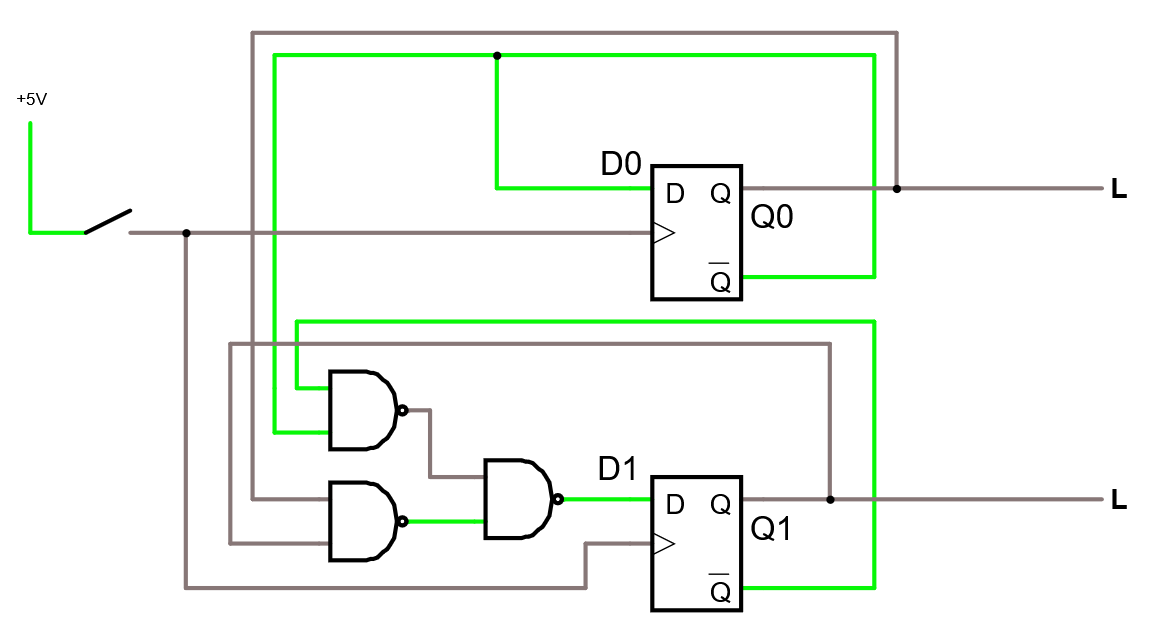
Som du ser i simulatorn, har funktionen inte förändrats.
T -vippor
Säg att vi hade haft T -vippor istället.
| Q1 | Q0 | T1 | Q1+ | T0 | Q0+ |
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 0 | ||
| 1 | 0 | 0 | 1 | ||
| 1 | 1 | 1 | 0 |
Vad gör en T-vippa? Den flippar utgången Q om ingående T = 1. Om vi tittar på första raden som exempel. Om Q1 = 0 från början och vi vill ha Q1+ = 1, då måste signalen flippas dvs T1 = 1. Men på rad 2 t.ex., där är Q1 = 0 från början och Q1+ = 0, där ska vi inte flippa något alls, dvs T1 = 0. Vi kan gå igenom hela tabellen ...
| Q1 | Q0 | T1 | Q1+ | T0 | Q0+ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
Nu ska fixa uttryck för T1 givet Q1 och Q0 och dito för T0. Vi ser snabbt att...
T1 = Q0 samt att T0 = 1
Det här blir otroligt enkel logik.
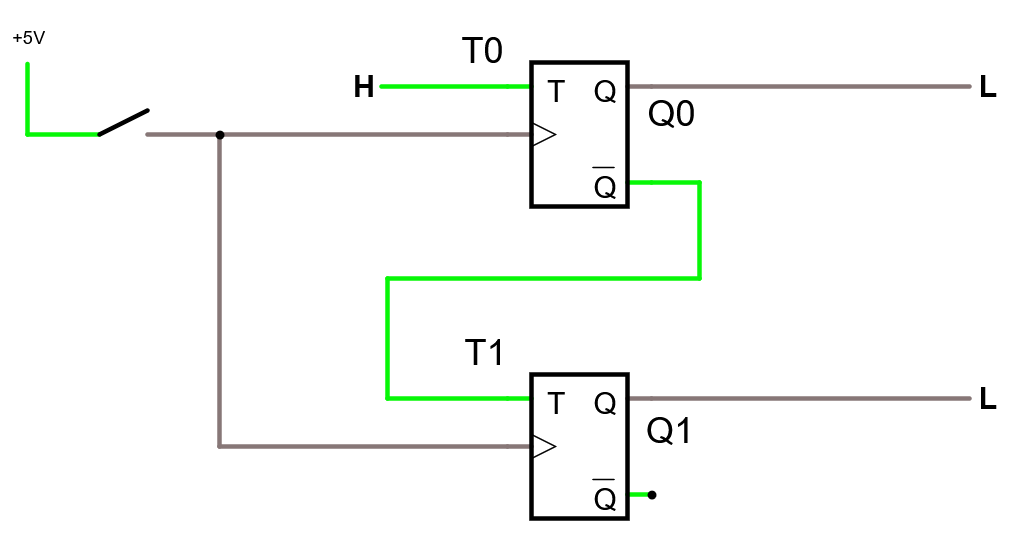
Studera funktionen i simulatorn.
JK -vippor
Om vi skulle göra ovanstående exempel med JK -vippor hade det blivit för enkelt. Du skapar en T-vippa genom att koppla ihop båda ingångarna på en JK -vippa, eller hur? Så, vi hittar på ett nytt exemel.
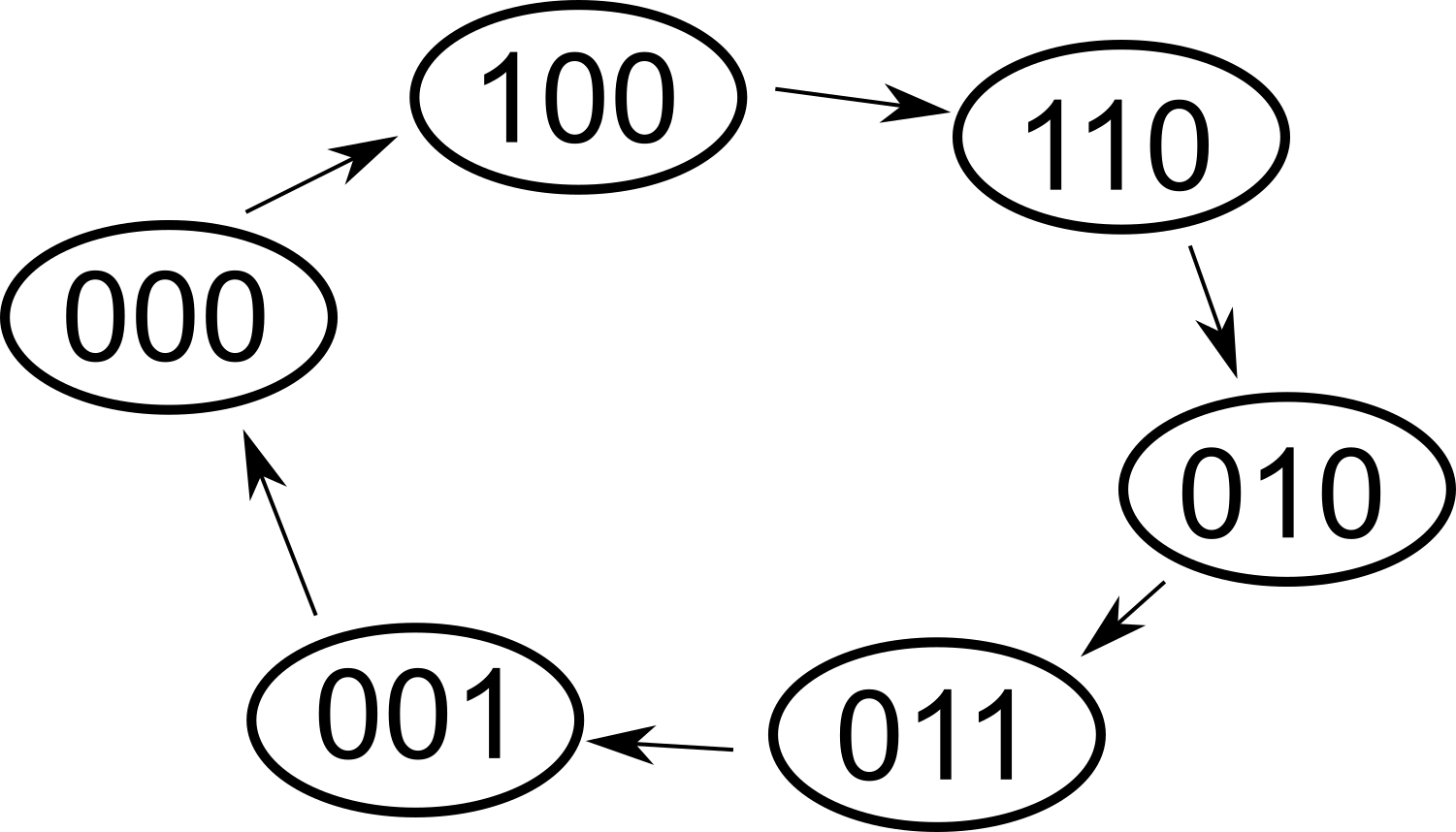
Säg att vi vill ha sekvensen 000,100,110,010,011,001,000,... dvs en 1:a som vandrar fram och tillbaka. Vi behöver 3 stycken vippor, t.ex. 3 stycken JK -vippor. 3 stycken vippor, då finns det 8 kombinationer att beakta inledningsvis.
| Q2 | Q1 | Q0 |
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
Så suddar vi ut allt detta, fixar fler kolumner och stoppar in våra tillstånd, 000,100,110,010,011,001,000,...
| Q2 | Q1 | Q0 | Q2+ | Q1+ | Q0+ |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Vi lägger nu in kolumner för JK -vipporna eftersom vi glömde det. Så, om vi tittar på första raden nedan, där är Q2=0 och Q2+ = 1. Vad måste J2 och/eller K2 vara för att Q2 skall flippa över (eller sättas) från 0 till 1 ?
| Q2 | Q1 | Q0 | J2 | K2 | J1 | K1 | J0 | K0 | Q2+ | Q1+ | Q0+ |
| 0 | 0 | 0 | ? | ? | 1 | 0 | 0 | ||||
| 0 | 0 | 1 | 0 | 0 | 0 | ||||||
| 0 | 1 | 0 | 0 | 1 | 1 | ||||||
| 0 | 1 | 1 | 0 | 0 | 1 | ||||||
| 1 | 0 | 0 | 1 | 1 | 0 | ||||||
| 1 | 0 | 1 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 1 | 0 | ||||||
| 1 | 1 | 1 | 0 | 0 | 0 |
Om J=K=1 så är JK -vippan i flipp-mode, dvs den kommer invertera utgående. Samtidigt, om J=1 så är JK-vippan i SET -mode, dvs den sätter utgången Q=1. Om man funderar lite, så spelar det ingen roll om utgången blir 1 p.g.a. att man flippar 0 till 1 eller om man helt sonika sätter 1 på utgången. Eller hur?
Titta på nedan förslag. Struntsamma vad K2 är. Om K2=0, så kommer Q2+ bli 1. Om K2=1, så flippas Q2 till 1. Så vi kan sätta X på K2, dvs det spelar ingen roll vad K2 är.
| Q2 | Q1 | Q0 | J2 | K2 | J1 | K1 | J0 | K0 | Q2+ | Q1+ | Q0+ |
| 0 | 0 | 0 | 1 | x | 1 | 0 | 0 | ||||
| 0 | 0 | 1 | 0 | 0 | 0 | ||||||
| 0 | 1 | 0 | 0 | 1 | 1 | ||||||
| 0 | 1 | 1 | 0 | 0 | 1 | ||||||
| 1 | 0 | 0 | 1 | 1 | 0 | ||||||
| 1 | 0 | 1 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 1 | 0 | ||||||
| 1 | 1 | 1 | 0 | 0 | 0 |
Samma resonemang på rad 2. Det viktiga är att Q0+ blir 0. Om Q0 flippas från 1 till 0, eller Q0 blir noll, därför att vi sätter K0=1 (reset), det spelar ingen roll.
| Q2 | Q1 | Q0 | J2 | K2 | J1 | K1 | J0 | K0 | Q2+ | Q1+ | Q0+ |
| 0 | 0 | 0 | 1 | x | 1 | 0 | 0 | ||||
| 0 | 0 | 1 | x | 1 | 0 | 0 | 0 | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | ||||||
| 0 | 1 | 1 | 0 | 0 | 1 | ||||||
| 1 | 0 | 0 | 1 | 1 | 0 | ||||||
| 1 | 0 | 1 | 0 | 0 | 0 | ||||||
| 1 | 1 | 0 | 0 | 1 | 0 | ||||||
| 1 | 1 | 1 | 0 | 0 | 0 |
Med motsvarande resonemang kan vi sedan fylla i resten av tabellen.
| Q2 | Q1 | Q0 | J2 | K2 | J1 | K1 | J0 | K0 | Q2+ | Q1+ | Q0+ |
| 0 | 0 | 0 | 1 | x | 0 | x | 0 | x | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | x | 0 | x | x | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | x | x | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | x | 1 | x | x | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | x | 0 | 1 | x | 0 | x | 1 | 1 | 0 |
| 1 | 0 | 1 | x | 1 | 0 | x | x | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | x | 1 | x | 0 | 0 | x | 0 | 1 | 0 |
| 1 | 1 | 1 | x | 1 | x | 1 | x | 1 | 0 | 0 | 0 |
Några tillstånd inträffar aldrig. Vi hade kunnat ta bort dem från början, men bättre sent än aldrig. Vi sätter x på dessa tillstånd.
| Q2 | Q1 | Q0 | J2 | K2 | J1 | K1 | J0 | K0 | Q2+ | Q1+ | Q0+ |
| 0 | 0 | 0 | 1 | x | 0 | x | 0 | x | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | x | 0 | x | x | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | x | x | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | x | x | 1 | x | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | x | 0 | 1 | x | 0 | x | 1 | 1 | 0 |
| 1 | 0 | 1 | x | x | x | x | x | x | |||
| 1 | 1 | 0 | x | 1 | x | 0 | 0 | x | 0 | 1 | 0 |
| 1 | 1 | 1 | x | x | x | x | x | x |
Att vi satt X på signaler som inte spelar någon roll kommer hjälpa oss enormt mycket nu. Har du problem få fram de boolska uttrycken, använd t.ex. Quine McCluskey's metod från sanningstabell till logiskt uttryck eller karnaughdiagram. Men ibland är de också väldigt triviala.
J2 = Q2 Q1 Q0
K2 = Q1
J1 = Q2
K1 = Q0
J0 = Q1 Q2
K0 = Q1
Dvs, vi får följande kretsschema...
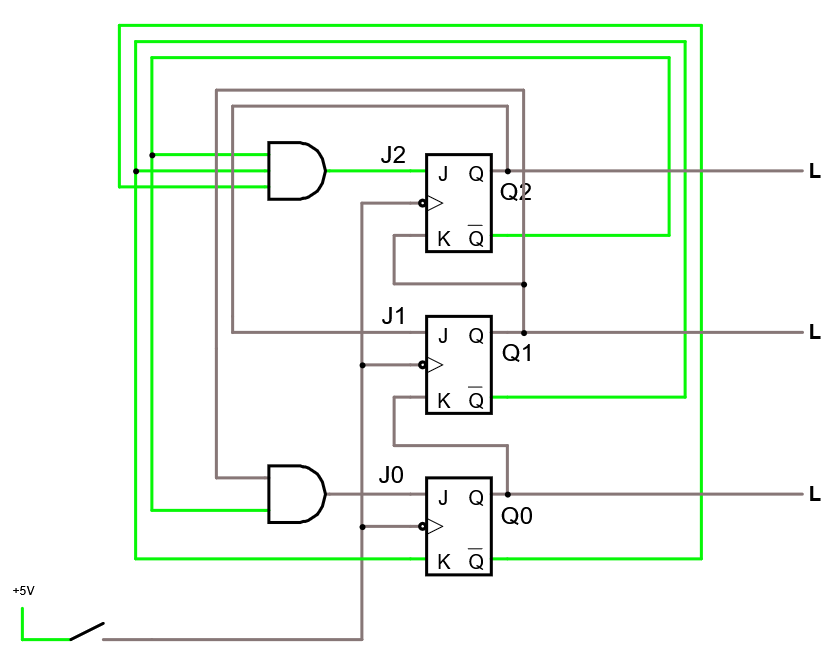
Testa sekvensnätet i simulatorn.