Växelström 1
Följande variabler och dess betydelse har du lite bekantskap med när denna webbsida är överstökad. Det är centralt för att senare kunna räkna med ohms lag även på växelströmskretsar.| a | Ögonblicksvärdet (momentanvärdet) |
| A | Effektivvärdet |
| ȃ | Toppvärdet (maximivärdet, amplituden) |
| ω | Vinkelfrekvensen i radianer per sekund |
| t | Tiden i sekunder |
| α | Fasvinkeln (anges typiskt i grader) |
AC/DC
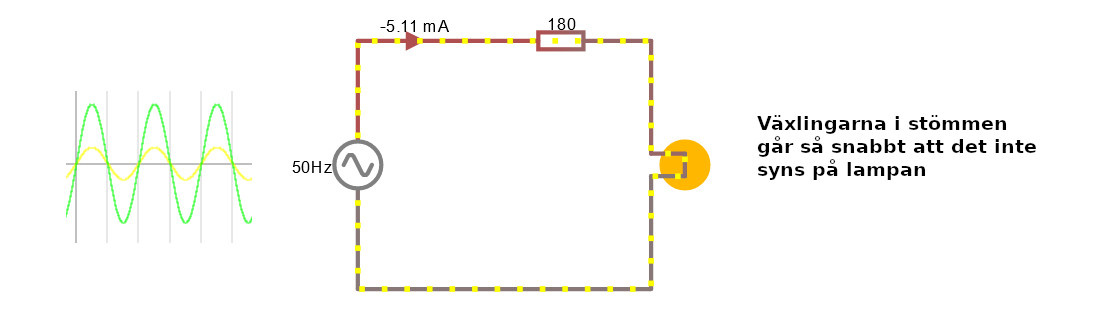
Men vad är egentligen växelström (AC = Alternating Current) ? Likström (DC = Direct Current) är att strömmen går i samma riktning i kretsen. Som från ett batteri. Det var där allting började. Voltastapeln, det är mitten på 1700-talet. Men växelström är att strömmen ändrar riktning med en viss frekvens. Vad sjutton kommer det ifrån?Klicka här för att öppna nedanstående simulering. Kurvan nedanför visar strömmen i kretsen som uppenbart byter riktning hela tiden.
 Vem har kommit detta? Vad är poängen med att byta riktning hela tiden?
Vem har kommit detta? Vad är poängen med att byta riktning hela tiden?När man producerar elektricitet med en generator på något sätt, dvs bygger en fysisk kontruktion med lindad koppartråd som utnyttjar att vi genom induktion kan få elektroner att röra på sig, då är det växelström man får från första början. Så AC är egentligen ingenting någon kommit på - utan snarare något som funnits där hela tiden, som vi utforskat. Läs mer om historien runt AC och DC. Det visade sig, när det kommer till elproduktion, att AC hade betydligt fler fördelar än vad DC hade. Bland annat att AC är enkelt att transformera upp och ner med en transformator. Denna "detalj" gjorde det möjligt att transformera upp spänningen till en väldigt hög spänning, vilket minskar effektförlusterna vid transport av elektricitet långa vägar. Så istället för att bygga en DC -kraftstation i varje kvarter som Edison gjorde, så kunde man bygga en stor kraftstation utanför staden och sedan transportera in elektriciteten i staden. Det var detta Tesla förslog man skulle göra. Edison och Tesla, de var verkligen inte vänner. Även om det var Edison som tjänade pengar, så var Tesla den som fick rätt, då han förstod fysiken.
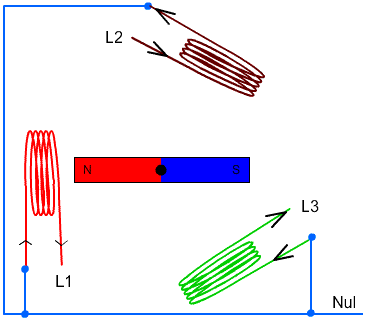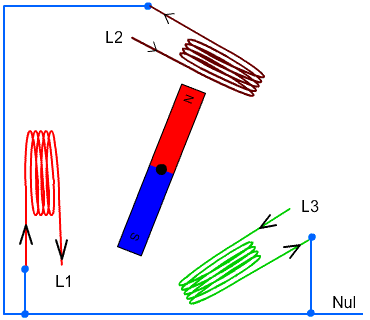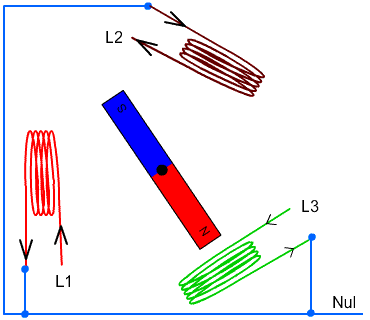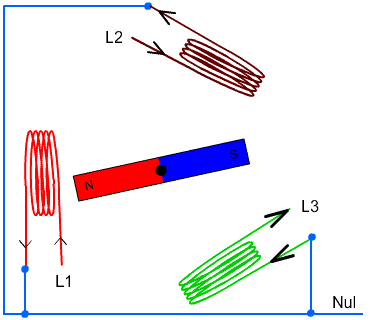
Studera nedan skiss hur elektricitet genereras genom att flytta en ledare i ett magnetfält. Utan kommutator, så är det växelström vi får. Med en kommutator kan vi se till att vi får likström.
Växelström är därför det vi har i våra vägguttag (220 Volt AC) idag. Det vanligaste är att vi använder oss av 2-fas växelström, men i sammanhang där man behöver lite högre effekt, där använder vi 3-fas växelström.
Frekvens (f), Period (T), Amplitud
Amplituden på vågen är mätt från 0 -nivån till max utslag. Så en signal som pendlar mellan -5 volt och +5 volt har alltså amplituden 5 volt. Tänk Amplitud = Absolutbeloppet. Vi mäter Perioden T (eller t) mellan omslagen och får då fram en tid, en periodtid eller våglängd. Det brukar mätas med T sek. Om vi inverterar värdet av periodtiden, T, då får vi frekvensen - alltså hur många sådana här omslag vi har för en viss tid.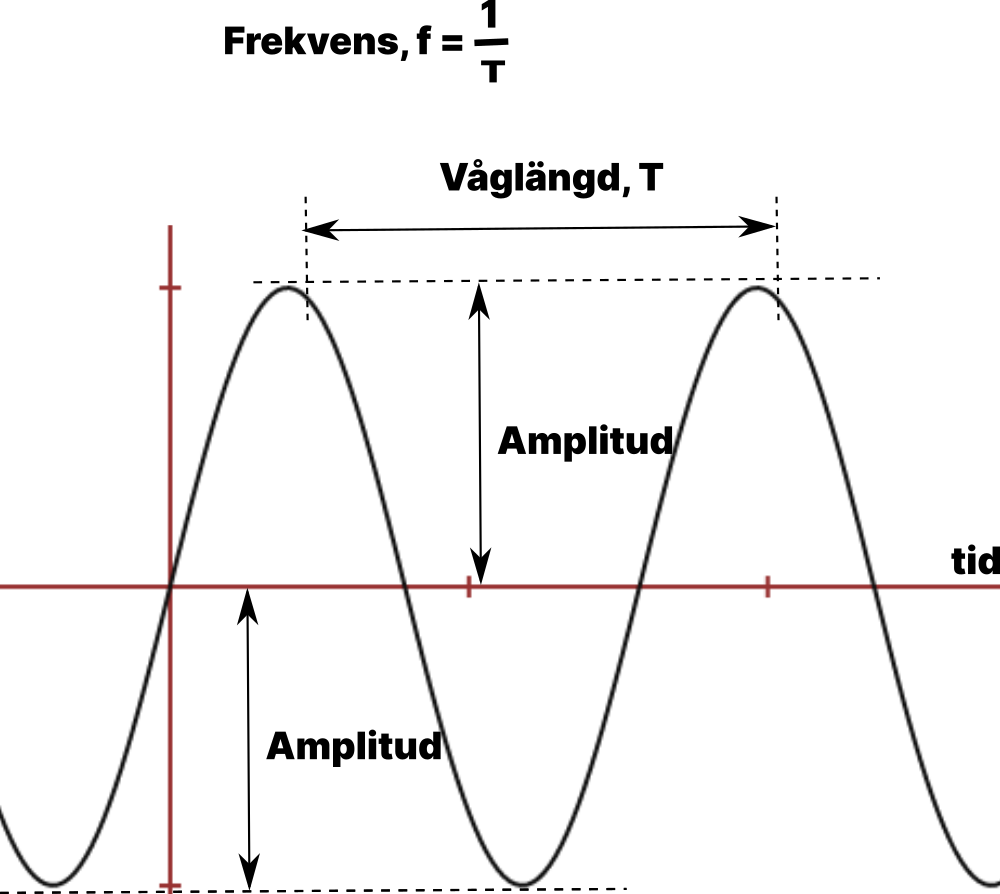
Om periodtiden är 2 hundradels sekunder, dvs T = 0.02 sek, då blir frekvensen f = 1/0.02 = 50 Hz. Det betyder 50 svängningar per sekund.
Detta är den frekvens vi har i våra vägguttag. Frekvensen är pyttelite lägre än 50 Hz när belastningen på elsystemet är hårdare och pyttelite över 50 Hz när det finns mer elektricitet än vi för tillfället behöver. Att det blir på detta sätt, det bror på att det är roterande generatorer som framställer elektriciteten. Är elsystemet hårt belastat, så är det tungt rotera generatorerna och hastigheten tenderar att minska pyttelite även om motåtgärder (mer vatten på turbiner etc.) utförs. Om belastningen på systemet minskar, då får generatorerna lite lättare att rotera. Du kan följa den exakta situationen på elsystemets belastning och frekvensen, t.ex. via denna webbsida.
En ljudvåg på 50 Hz är hörbar för människor, som en låg dov bas-ton. Musik innehåller typiskt frekvenser mellan 20 Hz och 15000 Hz.
En lägre frekvens svänger lite långsammare, period-tiden är längre.
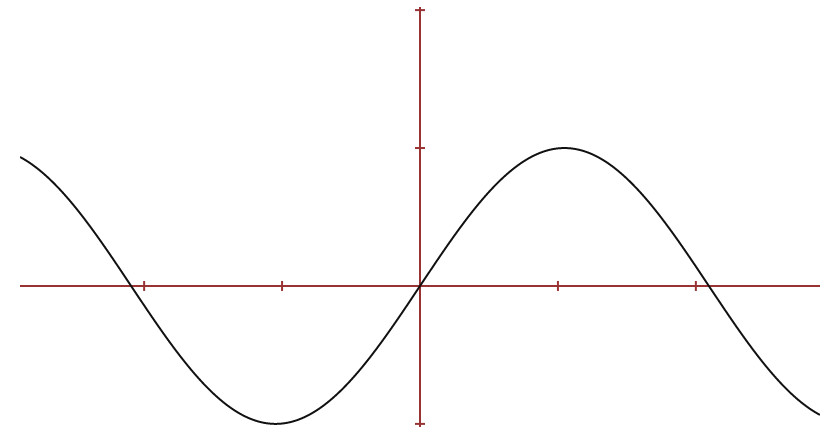
En högre frekvens svänger lite fortare, periodtiden är kortare.
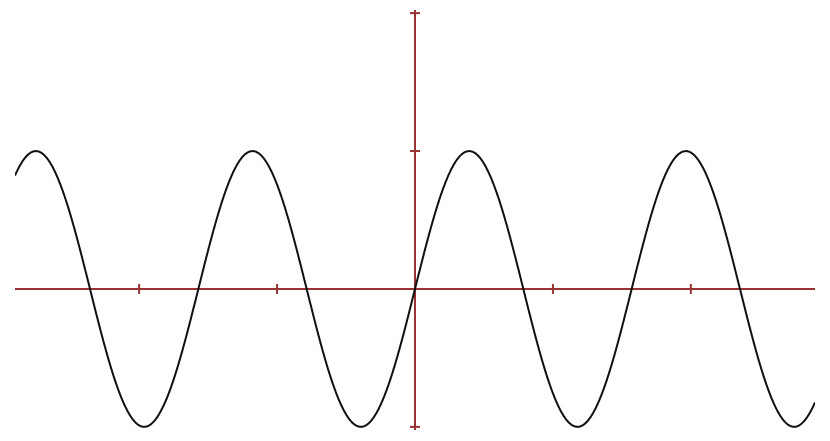
Vinkelfrekvens, ω = 2πf
När vi räknar på växelströmskretsar, då använder vi också ofta vinkelfrekvensen ω , som har enheten radianer per sekund. Vinkelfrekvensen räknas ut som ω = 2πf och enheten är radianer per sekund. Dvs, vet vi frekvensen, så vet vi vinkelfrekvensen. Och tvärtom.För att förstå vad vinkelfrekvens är, titta på den roterande visaren som skapar kurvan. Rotationen sker med en viss hastighet, visaren passerar ett visst antal radianer varje sekund. Vi kan välja att kalla hastigheten radianer per sekund. Kurvan flyter alltså fram med en hastighet som kan mätas i radianer per sekund.
Om vi tänker oss frekvensen 1 Hz, dvs att avståndet mellan 2 vågtoppar är 1 sekund, då är det samma sak som att vi roterat 1 varv på gradskivan på 1 sekund. Ett varv är 2π radianer. Vi räknar i radianer och då blir vinkelfrekvensen 2π = ca 6.28 radianer per sekund.
Om frekvensen är 50 Hz, då är vinkelfrekvensen ω = 2π*50 = 314 rad/sek. Vi återkommer även till detta lite senare. 2π radianer är samma sak som 360 grader, dvs ett helt varv.
Fasvinkel
Fasvinkel är alltså den vinkel som vågen är ur fas med själva diagrammet eller fasskillnaden mellan 2 olika kurvor. Men vi börjar med en kurva, så tar vi 2 kurvor om en liten stund. Labba lite och utveckla lite känsla.En lite otypisk detalj här, i en annars ganska ordnad fysik och matematik, det är att vi använder ibland radianer och ibland grader. När vi räknar så använder vi radianer. Vinkelfrekvensens uttryck, ω = 2πf är uppenbart radianer - eller hur? Ett varv är 2π radianer. När vi pratar om en fasvinkel, då pratar vi grader eftersom det är mycket mer bekvämt säga 30 grader eller 90 grader fasförskjutning än vad det är att säga 0.5236 eller 1.57 radianers fasförskjutning. Som en konsekvens här, måste vi vara lite uppmärksamma på om vi behöver radianer eller grader i vår kalkyl. En tumregel är att vi alltid pratar om grader - vi säger att kurva A är 30 grader fasförskjuten mot kurva B - men sedan räknar med radianer - dvs vi måste räkna om till radianer när vi räknar.
Toppvärde, Medelvärde, Effektivvärde (RMS)
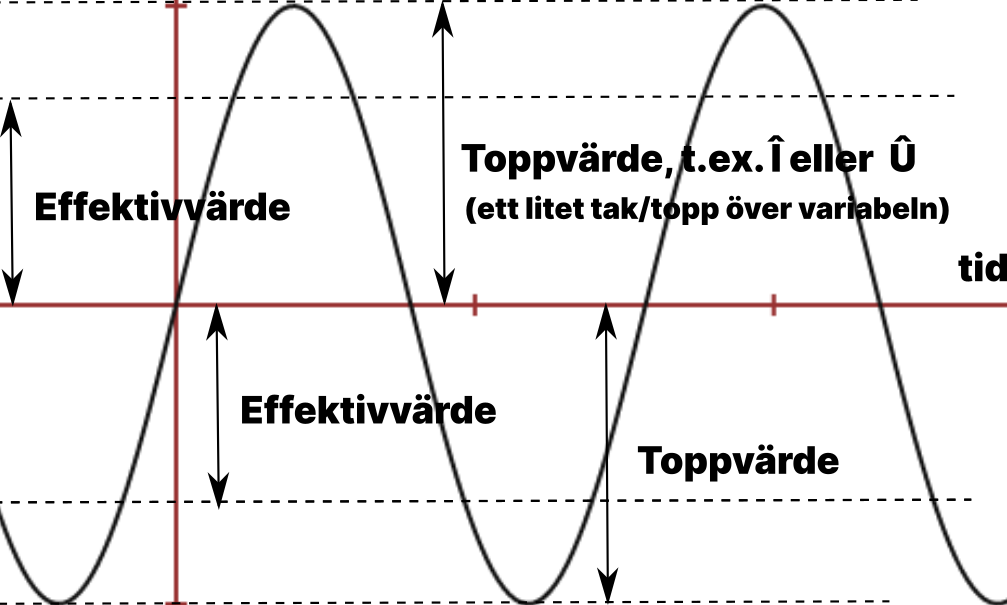
Toppvärdet ȃ är helt enkelt vågens amplitud. Ögonblicksvärdet, det är där signalen befinner sig i en viss tidpunkt. Medelvärdet är precis som det låter, signalens medelvärde. En ren sinus-signal har ett medelvärde på 0 volt. Medelvärdet används inte så ofta.Men vad är effektivvärde A? Effektivvärdet minns kanske lättast genom att tänka sig effektivvärde, dvs att det handlar om effekt.
Vi vill veta vilken nivå på växelspänning som ger exakt samma effektutveckling i en resistor som en likspänning gör. Det får vi veta om vi använder det kvadratiska medelvärdet på växelspänningen (RMS).
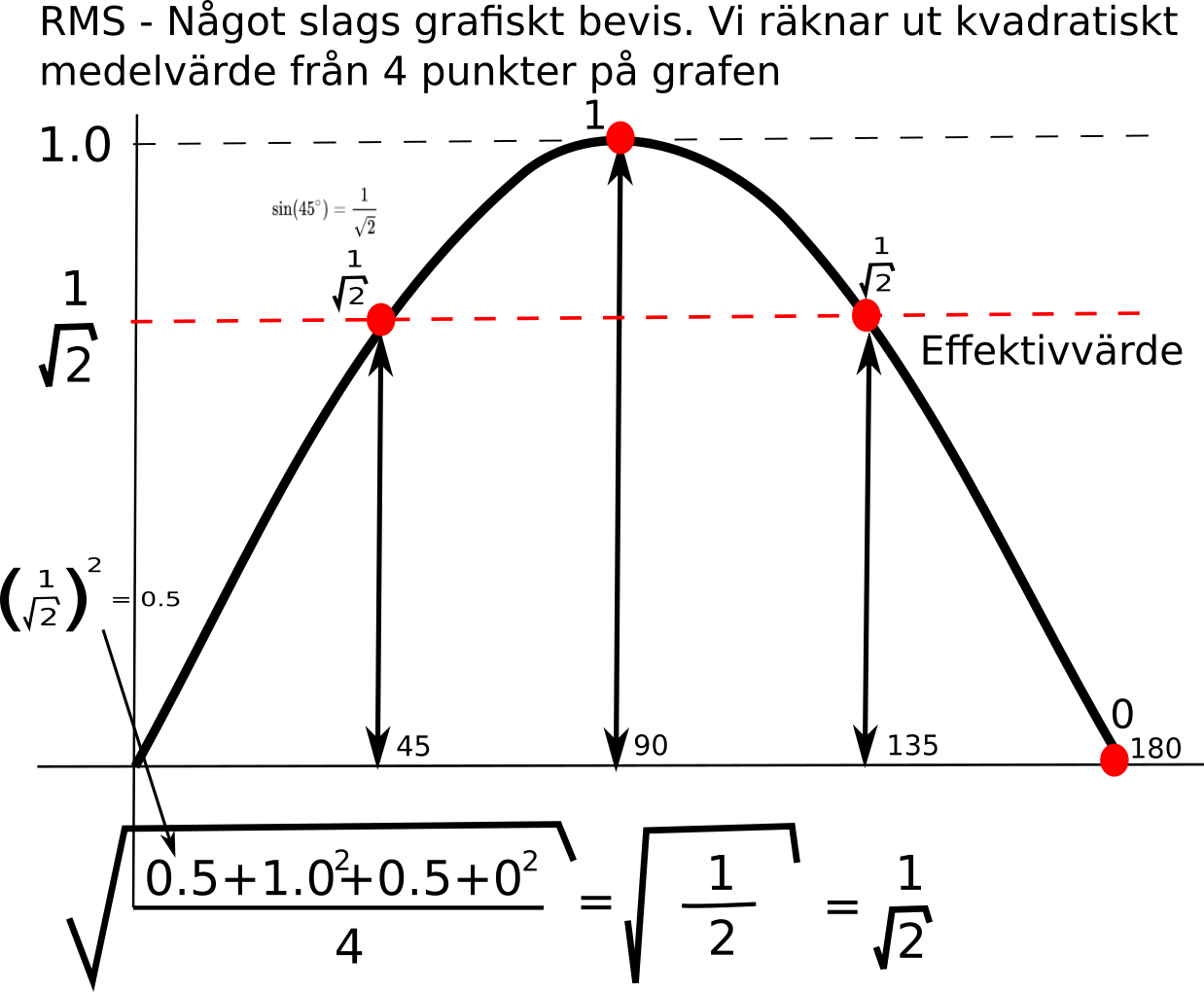
Effektivvärdet = Toppvärdet / √2
Säg att vi har en transformator och kör växelspänningen in i en helvågs likriktare.
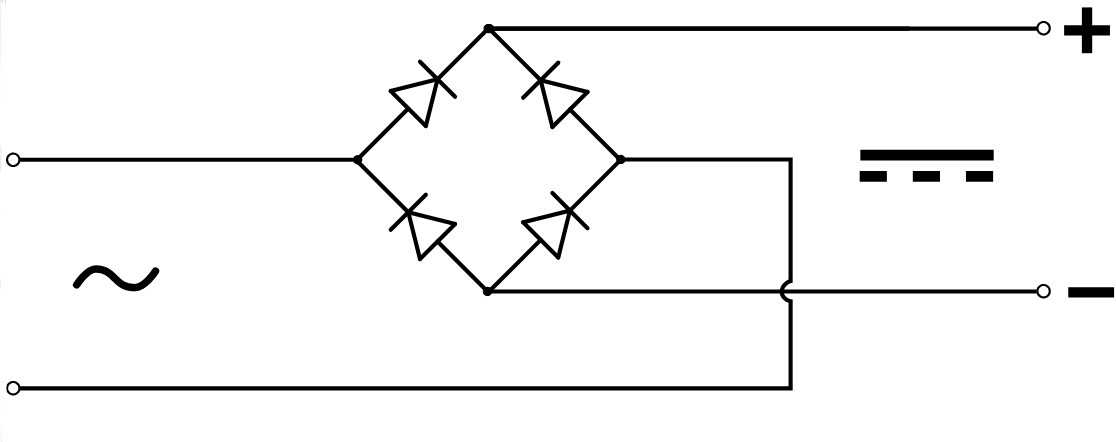
Signalen in i likriktaren har vi till vänster nedan och ut från likriktaren till höger.
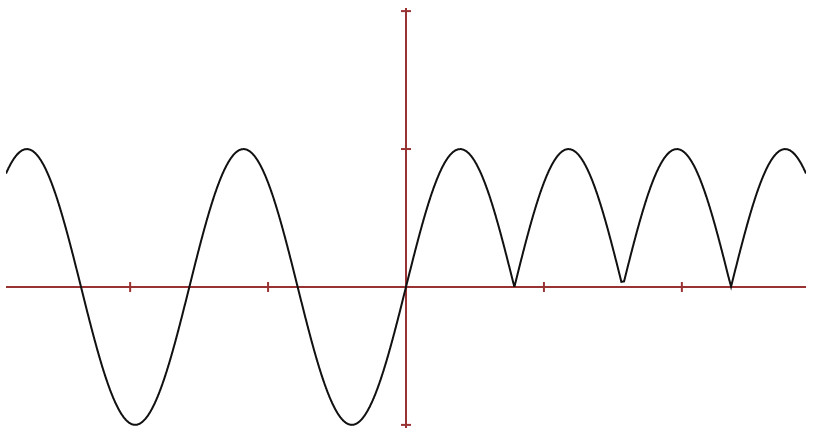
På grund av sinusvågens natur, så varierar energimängden upp och ner med spänning och ström. Kan vi göra någonting åt denna situation? Vi kan montera en kondensator på utgången. Denna kondensator kommer ladda upp sig när spänningen toppar och ladda ur sig när spänningen är kort, dvs i dalarna.
Ett sätt att betrakta det visuellt, förutsatt att man håller isär medelvärde och effektivvärde, för att "se" vad som händer, är att se det som nedan. I topparna laddas kondensatorn och i dalarna laddas kondensatorn ur.
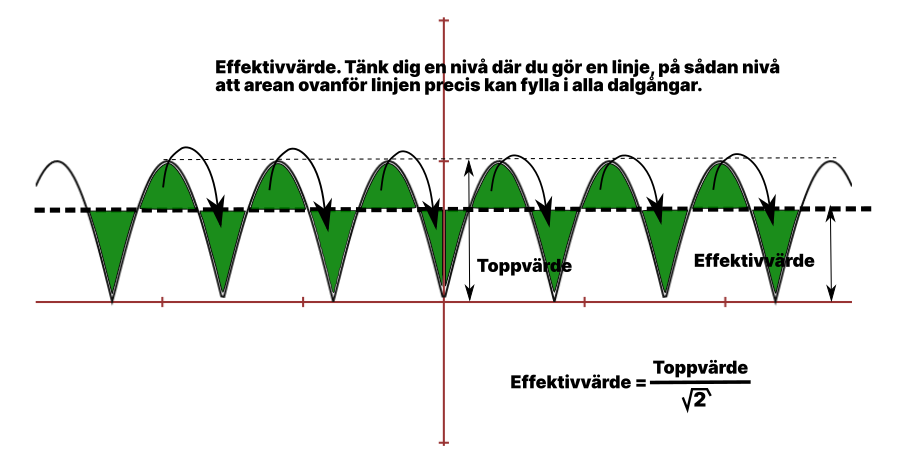
För att driva någonting som drar 12 volt, så måste alltså transformatorn innan likriktaren vara på 12*√2 = 17 volt. Med en transformator på 17 volt, kommer vi alltså kunna driva något på 12 volt.
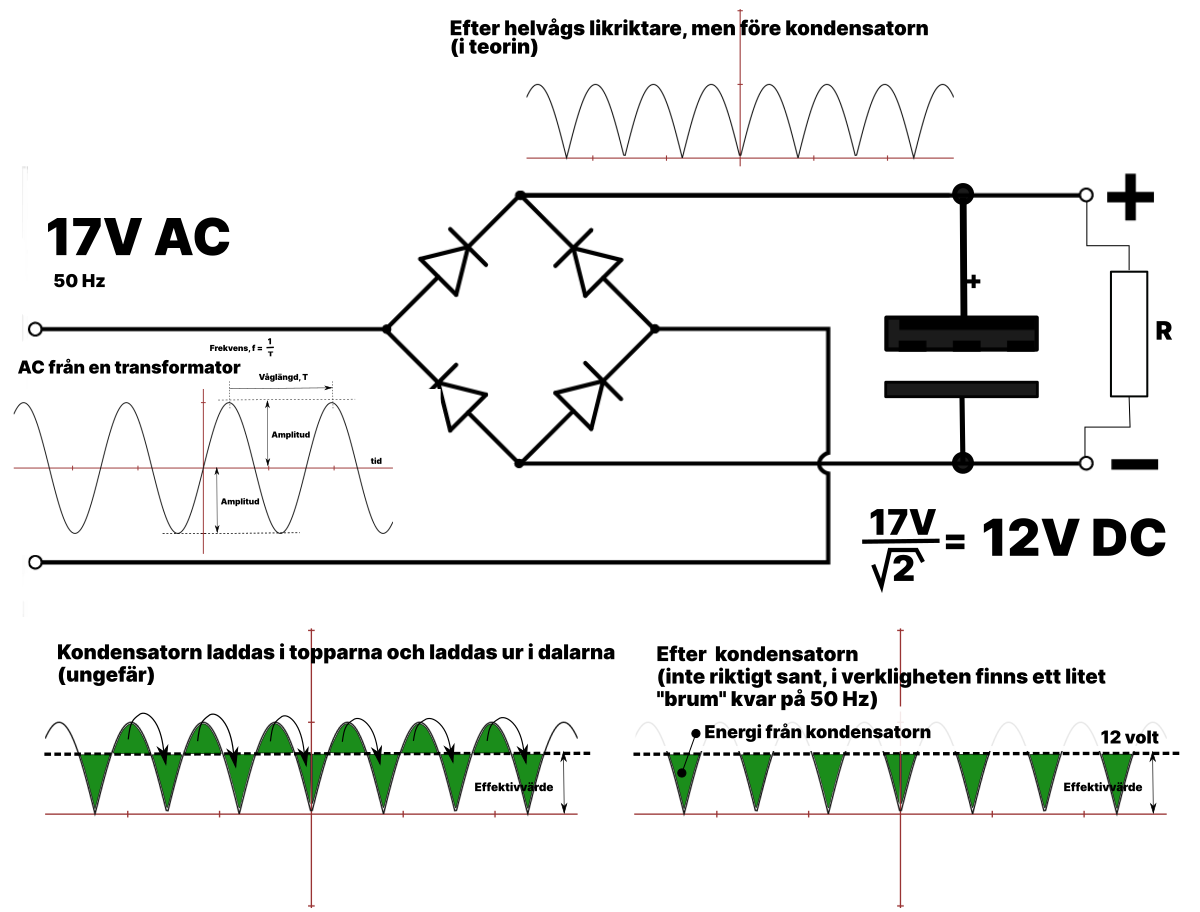
Verkligheten är inte lika ideal som teorin. I verkligheten så finns fortfarande en del brum kvar i DC -spänningen med en sådan här lösning, dvs kondensatorn fyller inte tomrummet helt. Det kommer inte vara något problem om konstruktionen ska driva lampor eller en motor. Skall transformatorn driva en förstärkare kan denna konstrueras så att detta brum/rippel neutraliseras.
Studera följande krets i krets-simulatorn. Titta speciellt på utgångs-spänningen och notera det rippel som finns på utgången Om vi minskar lasten, så blir ripplet mindre.
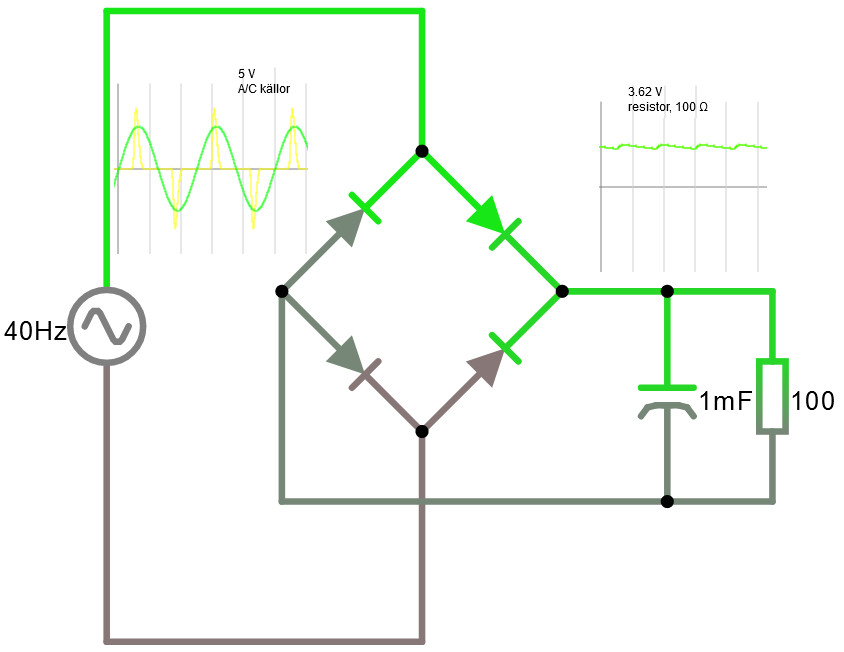
Studera helvågslikriktaren med en glättningskondensator på utgången. Utspänningen med denna lösning blir:
UDCut = UACin / √2
2 stycken sinusvågor
Säg, att vi har 2 stycken sinusvågor.Vi kan summera dessa 2 sinusvågor grafiskt, med visarmetoden - fasdiagram. Ändra värden ovan och testa. Jag ska förklara hur detta fungerar, strax. Den svarta grafen är summan av den gröna och röda.
Kan vi summera dem utan vidare? Det kan vi. Summan av flera sinusvågor blir en ny sinusvåg. Labba med ovanstående grunka ett tag. Genom att summera vektorerna som olika sinusvågor representerar, får vi en vektor som representerar summan. Visst är det vackert i sin matematiska enkelhet. Det gäller bara att se mönstret.
Lite längre fram när vi använder visarmetoden, så skippar vi den här snurrande tjusiga illustrationen, som jag snickrat på en hel vecka, och skissar enbart vektorerna. Men nu vet du vad som döljer sig bakom visarmetoden i skolboken, när du ser den nästa gång.
Efter denna visuella introduktion till begreppet växelström är du redo för lite mer matematik. :-) Växelström del 2. Som dyker upp någon annan dag. :)