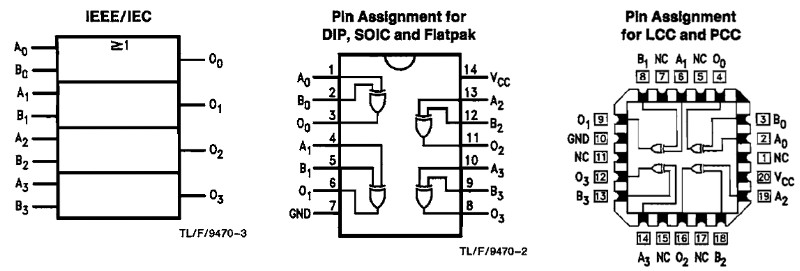
Kombinatorisk logik
1 och 0, hög och låg
Så, vi har med 1:or och 0:or att göra, inget annat (vanligtvis). Ibland säger man "hög" och menar då "1". I konsekvensens namn säger man då "låg" och menar "0". En låg signal är oftast ganska nära 0 volt. En hög signal är vanligtvis i närheten av 5 volt, men kan också vara i närheten av t.ex. 3.3 volt. Det beror lite på vad det är för kretsar. Om en krets med 5 volts -logik skall kommunicera med en krets med 3.3 volts -logik, då behöver man någon typ av konvertering däremellan. Är man riktigt våghalsig och en människa med mycket tur, och signalen enbart rör sig mot 3.3 volts -logiken så funkar det ibland att koppla ihop 5 volt med 3.3 volts -logik. Men det är inte så man ska bygga apparater som håller en människa vid liv på ett sjukhus.
Egenskaper
Man kan dela in logiska nät i kombinatorisk logik, dvs logiska nät där signalen enbart rör sig mot utsignalen, och sekventiell logik, där utsignalen på minst ett ställe återkopplas till en insignal tidigare i nätet. Exempel på sistnämda är t.ex. olika typer av flip-flop som växlar mellan 2 tillstånd.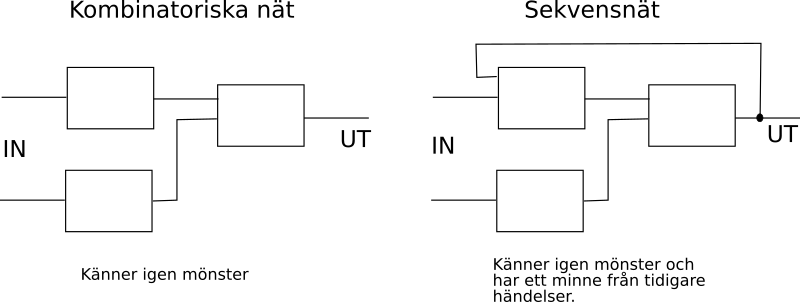
Ett kombinatoriskt nät ger alltid en viss utsignal givet en viss insignal. Svårare än så är det inte. En viss kombination av insignaler ger en viss utsignal. Om du har en tabell med insignaler och utsignaler, så kan du använda dig av smarta verktyg för att tillverka ett kretschema, t.ex. Karnaugh -diagram eller Quine McCluskeys algoritm. Men låt oss ta det från början!
Boolsk funktion och boolsk algebra
Kretsar som utför logiska operationer och matematik som beskriver densamma är 2 sidor av samma grej. Grunden för boolsk algebra och motsvarande logiska kretsar är följande:OCH
A = X∧Y vilket är samma som A = X & Y, där A är 1 enbart om både X och Y är 1. Man kan se det som multiplikation. 1*1 = 1, om någon av termerna är noll så blir produkten 0. Eller hur?ELLER
A = X∨Y vilket betyder X eller Y, där A blir 1 om någon av X eller Y är 1. Man kan se det som plus. Om någon av termerna är 1 så blir summan 1 (det blir ju förstås 2 egentligen, men vi säger 1). Om båda termerna är noll så blir summan noll.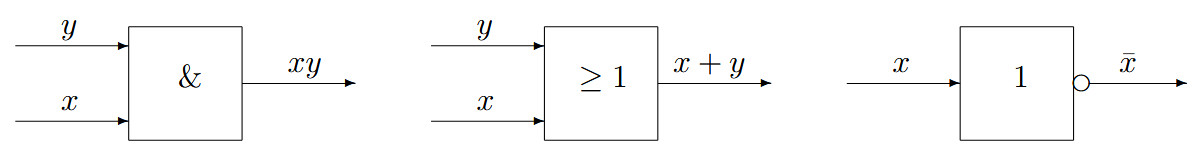
Logiksymboler
För att kunna rita elektriska nät med logikkretsar, har vi ett gäng symboler att förhålla oss till.| Not | 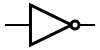 |
X = A | |
| AND | 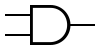 |  | X = A∧B |
| OR | 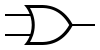 | 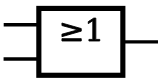 | X = A∨B |
| NAND |  | X = A∧B | |
| NOR | 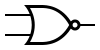 |
X = A∨B | |
| XOR | 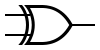 | X = A⊕B | |
| XNOR | 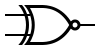 | X = A⊕B |
Inverteraren
Den enklaste typen av grind, en inverterare.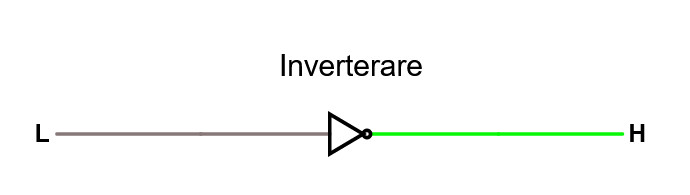
Studera en inverterare i simulatorn. Klicka på insignalerna för att ändra dem. En inverterare tar alltså en digital hög signal och producerar motsatsen, dvs en hög blir låg och en låg blir hög.
En sanningstabell för inverteraren blir ganska enkel.
| In | Ut |
| 1 | 0 |
| 0 | 1 |
AND -grinden
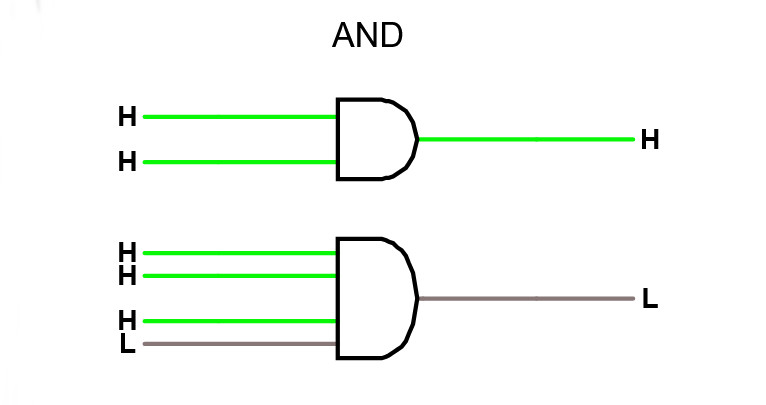
Studera en AND -grind i simulatorn. AND -grinden producerar hög utsignal om samtliga insignaler är höga. Om någon insignal är låg, så blir utsignalen låg.
Insignalerna på ovan grindar skulle kunna skrivas som X∧Y och A∧B∧C∧D.
En sanningstabell för AND -grinden ser alltså ut såhär, där Q = X∧Y.
| X | Y | Q |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Om vi har 3 signaler och önskar hög utsignal (Q) ifall samtliga 3 insignaler är höga, så ser det ut såhär.
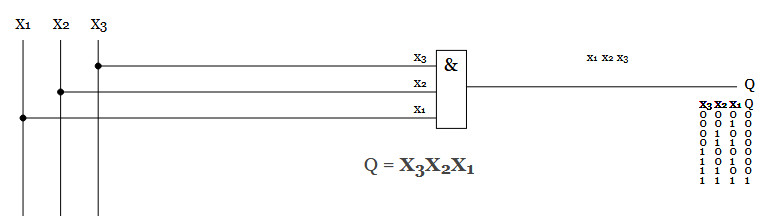
Om vi har 3 signaler och önskar hög utsignal (Q) ifall samtliga 3 insignaler är låga, så ser det ut såhär. Dvs, vi inverterar helt enkelt insignalen, så att 0 blir 1.
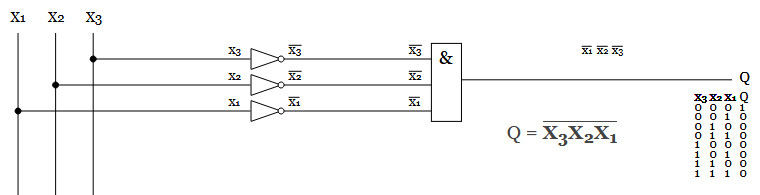
Om vi önskar en hög utsignal ifall X1 och X2 är höga men X3 är låg, så ser det ut såhär.
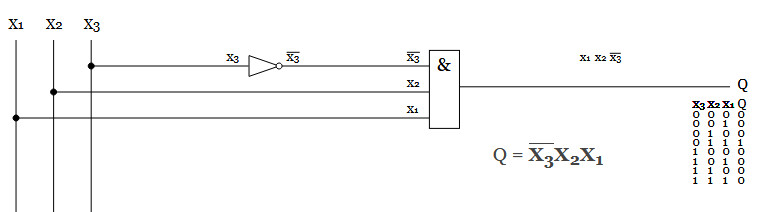
OR -grinden
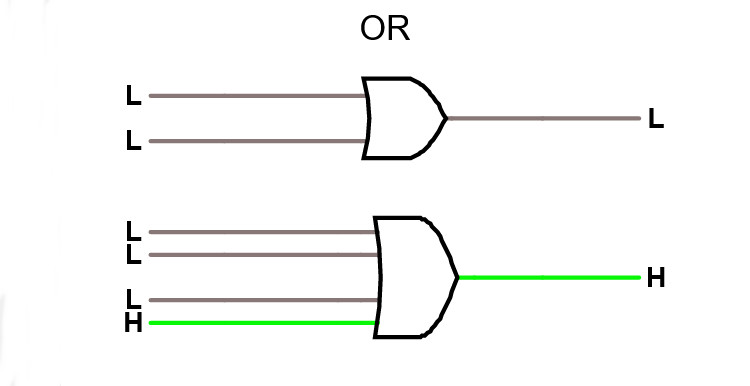
Studera en OR -grind i simulatorn. OR -grinden producerar hög utsignal om någon av insignalerna är höga, annars låg.
Insignalerna på ovan grindar skulle kunna skrivas som X∨Y och A∨B∨C∨D.
En sanningstabell för OR -grinden ser alltså ut såhär, där Q = X∨Y
| X | Y | Q |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Om vi har 3 insignaler och vi önskar hög utsignal ifall någon (minst 1) av 3 signaler är höga, så ser det ut såhär.
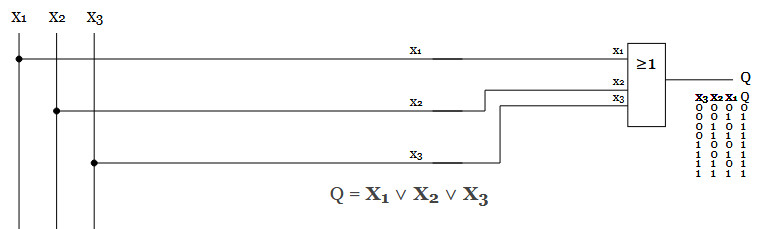
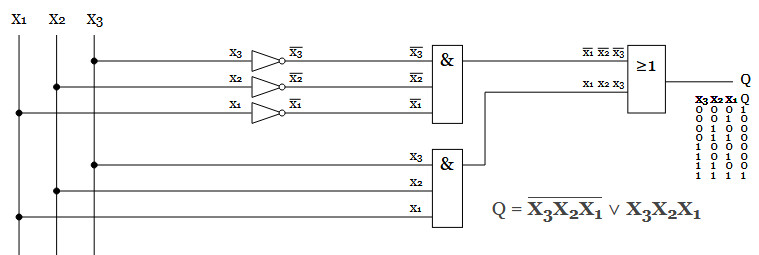
Om vi har 3 insignaler och vi önskar hög signal ifall alla 3 signaler X1 och X2 och X3 är höga eller alla 3 signaler är låga, så kan vi göra såhär.
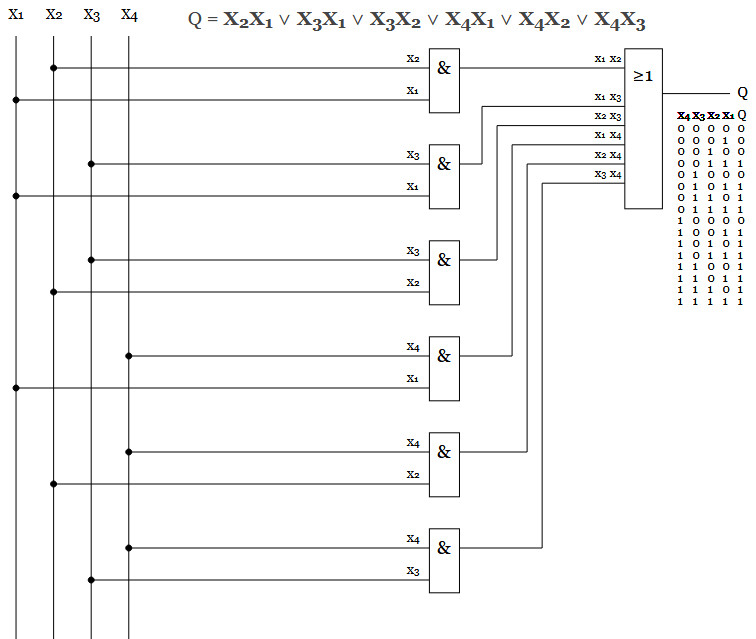
Om vi önskar en hög utsignal ifall minst 2 stycken av signalerna X1 - X4 är höga, så kan det se ut såhär.
NAND -grinden
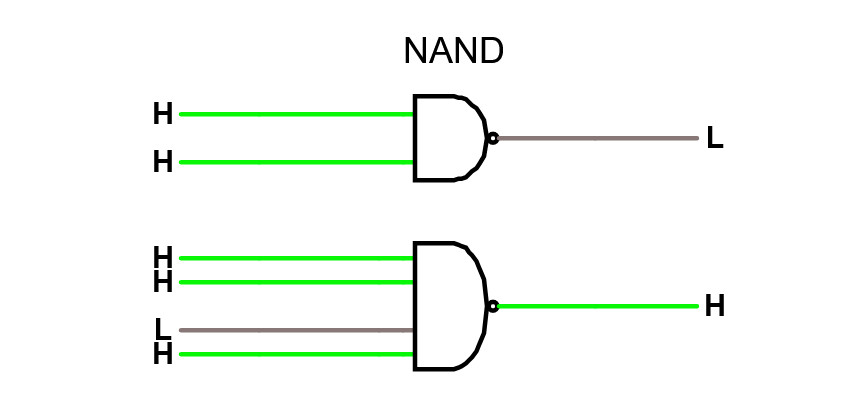
Studera en NAND-grind i simulatorn. En NAND -grind fungerar som en AND -grind, förutom detaljen att utsignalen inverteras.
Insignalerna på ovan grindar skulle kunna skrivas som X∧Y och A∧B∧C∧D.
En sanningstabell för NAND -grinden ser alltså ut såhär, där Q = X∧Y
| X | Y | Q |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
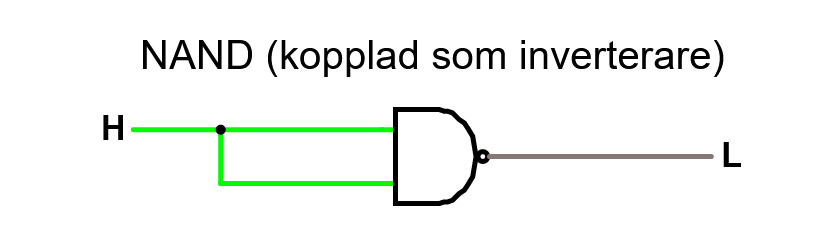
En NAND -grind kan enkelt kopplas till att bli en inverterare.
NOR -grinden

Studera en NOR -grind i simulatorn. En NOR -grind fungerar som en OR -grind förutom att utsignalen inverteras.
Insignalerna på ovan grindar skulle kunna skrivas som X∨Y och A∨B∨C∨D.
En sanningstabell för NOR -grinden ser alltså ut såhär, där Q = X∨Y
| X | Y | Q |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
Om vi önskar en hög utsignal ifall samtliga insignaler är låga, så kan det se ut såhär.
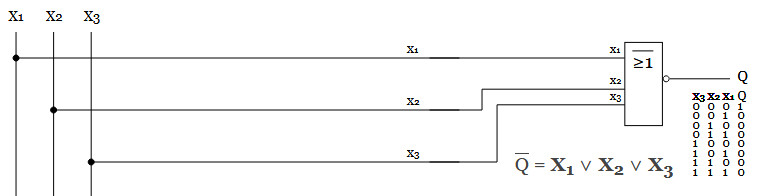
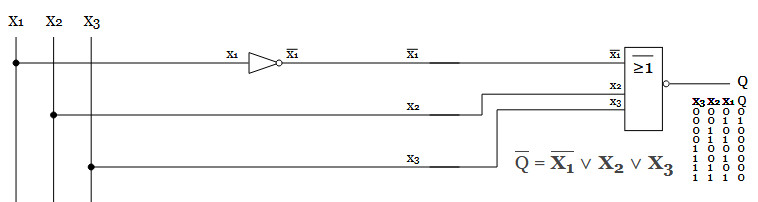
I detta fall kommer utsignalen att bli låg omX2 och X3 är låga och X1 är hög.
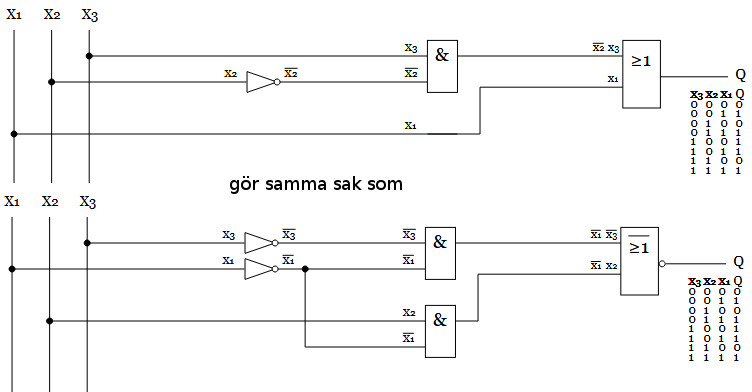
Nedan 2 nät ger samma utsignaler givet samma insignaler. Vad vi väljer för grindar påverkar om nätet blir mer eller mindre komplicerat.
XOR -grinden ⊕
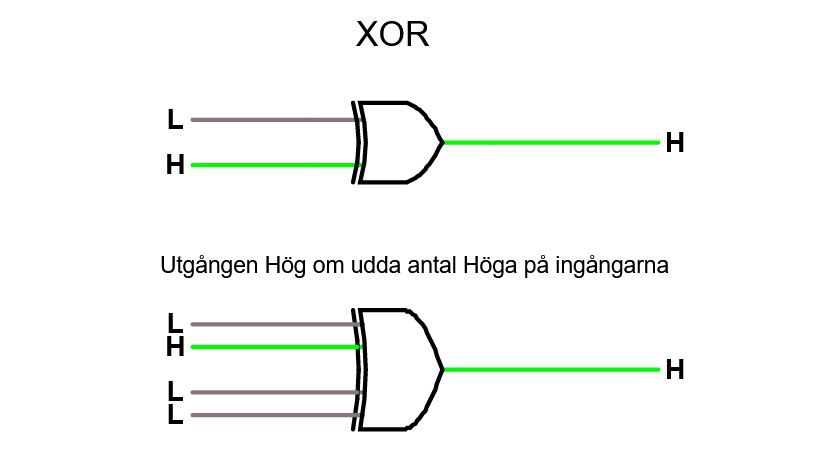
Studera en XOR -grind i simulatorn. XOR är lite speciell och har en stor användning inom matematik med binära tal. Vad XOR gör är att grinden producerar hög utsignal om en av ingångarna är hög - annars låg utsignal. Dvs, generellt producerar XOR hög utsignal om ett udda antal av ingångarna är höga.
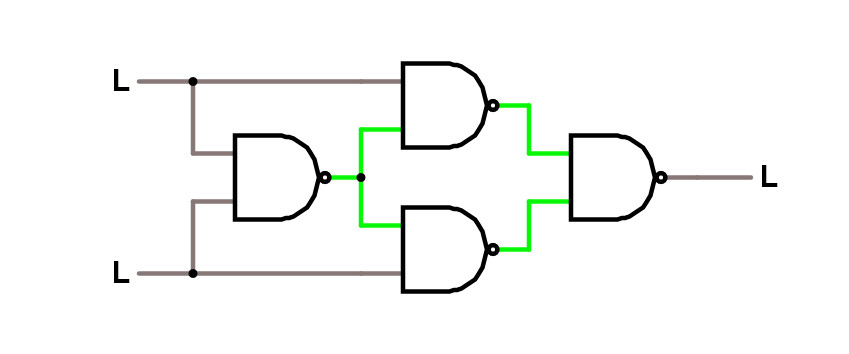
Studera hur en XOR -grind kan byggas med NAND -grindar i simulatorn. En XOR -grind kan byggas med 4 stycken NAND -grindar.
Insignalerna på ovan grind skulle kunna skrivas som X⊕Y.
En sanningstabell för XOR -grinden ser alltså ut såhär, där Q = X⊕Y
| X | Y | Q |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Godtyckliga nät
Vi kan förstås kombinera ovan gridar i all oändlighet för att få ett visst önskvärt resultat. Vanligtvis existerar förstås lite konkreta önskemål runt vilket resultat som önskas. Dvs, vi har kanske 3-4-5 insignaler och givet ett visst eller vissa mönster på dessa signaler vill vi ha en viss utsignal. Så vi kan t.ex. göra en käck tabell. Dvs, precis som sanningstabellerna för en viss grind eller logisk funktion, så skapar vi en sanningstabell över vårt önskvärda logiska nät.| n | X1 | X2 | X3 | f(X1, X2, X3) | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 2 | 0 | 1 | 0 | X | 3 | 0 | 1 | 1 | 1 | 4 | 1 | 0 | 0 | 0 | 5 | 1 | 0 | 1 | 0 | 6 | 1 | 1 | 0 | X | 7 | 1 | 1 | 1 | 1 |
Vi kan också skriva detta på andra sätt, som t.ex. f-1(1) = {3, 7} som betyder "de signaler som ger 1 som utsignal" (on-set) eller f-1(0) = {0, 1, 4, 5} som betyder "de signaler som ger 0 som utsignal" (off-set) eller f-1(-) = {2, 6} som betyder "de signaler som ger ointressant utdata" (don’t care-set). Observera att don’t care ibland skrivs med ett streck - och ibland X.
Det är normalt de kombinationer som ger 1 som är de vi intresserar oss för.
I ovan tabell ser vi att om X1 är låg samtidigt som X2 och X3 är hög, så önskar vi 1 som resultat. Eller om X1, X2 och X3 samtidigt är höga så önskar vi också 1 som signal. Vi kan skriva detta som
f(X1, X2, X3) = X1X2X3 ∨ X1X2X3.
Om vi kallar vår utsignal för Q så kan vi också skriva
Q = X1X2X3 ∨ X1X2X3.
Det är viktigt vara på det klara varför denna funktion ger 1 som resultat för önskvärda värden på X1, X2 och X3.
| n | minterm | X1 | X2 | X3 | f(X1, X2, X3) | 0 | X1X2X3 | 0 | 0 | 0 | 0 | 1 | X1X2X3 | 0 | 0 | 1 | 0 | 2 | X1X2X3 | 0 | 1 | 0 | X | 3 | X1X2X3 | 0 | 1 | 1 | 1 | 4 | X1X2X3 | 1 | 0 | 0 | 0 | 5 | X1X2X3 | 1 | 0 | 1 | 0 | 6 | X1X2X3 | 1 | 1 | 0 | X | 7 | X1X2X3 | 1 | 1 | 1 | 1 |
Om du inte begriper det, så måste läsa allting en gång till eller förstå det från annan håll. Dessa termer kallas mintermer och motsvaras av en rad i tabellen. Vi har alltså en summa av mintermer, en SOP "Sum Of Products" (summa av produkter). Bara så att vi får begreppen på plats.
Detta kallas för disjunktiv normalform och är alltså den funktion som ger oss ovanstående tabell. Disjunktiv betyder eller. Som du ser står det ∨ (eller) mellan varje term. Normalform kallas det därför att alla signaler är med, dvs X1, X2 och X3.
Summan av dessa mintermer är sällan optimal. Vi kan förenkla.
Q = X1X2X3 ∨ X1X2X3 = (X1 ∨ X1) ∧ X2X3 = X2X3
Det går att förkorta ännu mer, eftersom 2 av funktionen värde är don’t care och vi kan därför välja den utsignal på don’t care som passar oss bäst, t.ex. 1. Vi får därför följande:
Q = X2
Bekräfta att du förstår detta genom att titta på ovanstående tabell. Dvs, vi får vår önskvärda utsignal enbart genom att dra en sladd ifrån X2. Behövs ingen grind!
Om vi har en tabell, så finns utmärka verktyg för att skapa ett kretsschema utifrån denna tabell, t.ex. Quine McCluskeys algoritm eller genom att använda ett Karnaugh -diagram.
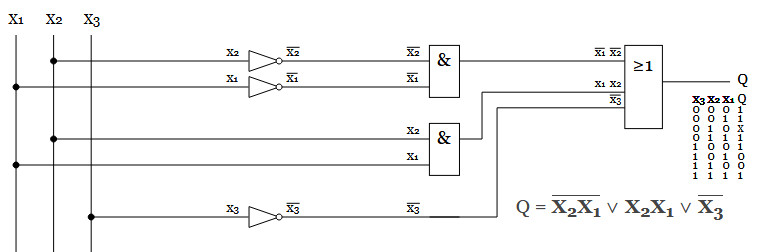
| n | minterm | X1 | X2 | X3 | f(X1, X2, X3) | 0 | X1X2X3 | 0 | 0 | 0 | 1 | 1 | X1X2X3 | 0 | 0 | 1 | 1 | 2 | X1X2X3 | 0 | 1 | 0 | X | 3 | X1X2X3 | 0 | 1 | 1 | 0 | 4 | X1X2X3 | 1 | 0 | 0 | 1 | 5 | X1X2X3 | 1 | 0 | 1 | 0 | 6 | X1X2X3 | 1 | 1 | 0 | 1 | 7 | X1X2X3 | 1 | 1 | 1 | 1 |
f(X1, X2, X3) =
= X1X2X3 ∨ X1X2X3 ∨ X1X2X3 ∨ X1X2X3 ∨ X1X2X3
= X2X1 ∨ X2X1 ∨ X3
Experimentera med egna tabeller
Prova själv här nedan genom att fylla i önskvärd utdata (dvs Q) för olika kombinationer av några insignaler och studera hur kretsschemat ser ut. Nedan är uträknat med Quine McCluskeys algoritm, som finns förklarad här.Antal variabler:
Använd en NOR -gate på utgången
 |
Ovan ger nedanstående kretsschema.
Du kan också skapa ett schema utifrån att fylla i ett Karnaugh -diagram. Vissa menar att Quine McCluskeys algoritm fungerar bättre när man har fler variabler, men eventuellt är Karnaugh -diagram snäppet enklare.
Kretsar

Kretsarna som gör detta möjligt finns i många olika varianter. Det intressanta här nedan är de sista 2-3 siffrorna på kretsen. Om du hittar en krets som gör det du vill göra, så skriver du ner dessa siffror innan du går till affären.
00 NAND (t.ex. 74LS00)
När någon av ingångarna är låg (L) så blir utgången hög (H).
02 NOR (t.ex. 74LS02 eller 4002)
När någon av ingångarna är hög så blir utgången låg (L).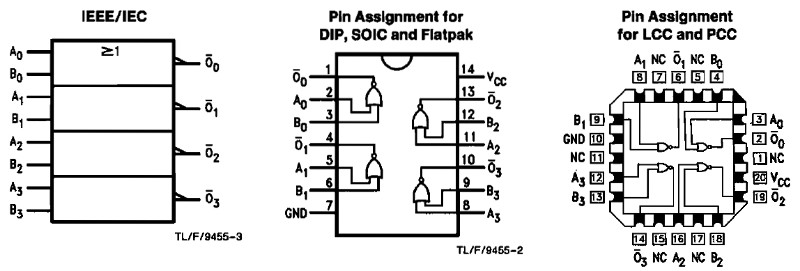
04 Hex Inverter (t.ex. 74LS04)
När en ingång är hög blir utgången låg och tvärtom.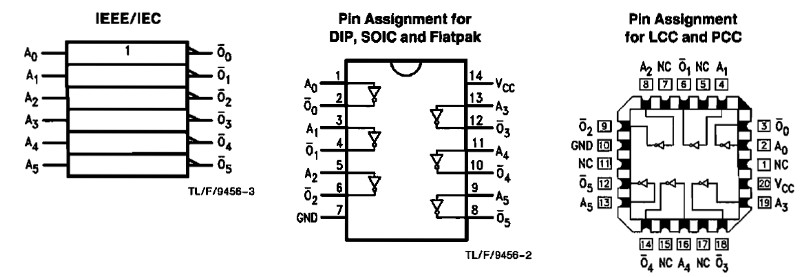
08 AND (t.ex. 74LS08)
Om alla ingångar är höga (H) så blir utgången hög (H).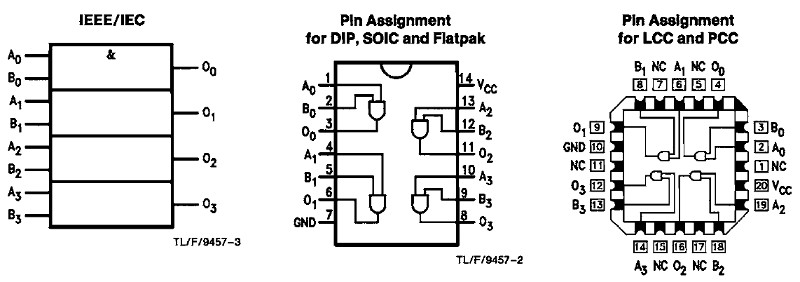
10 NAND (t.ex. 74LS10)
När någon av ingångarna är låg (L) så blir utgången hög (H).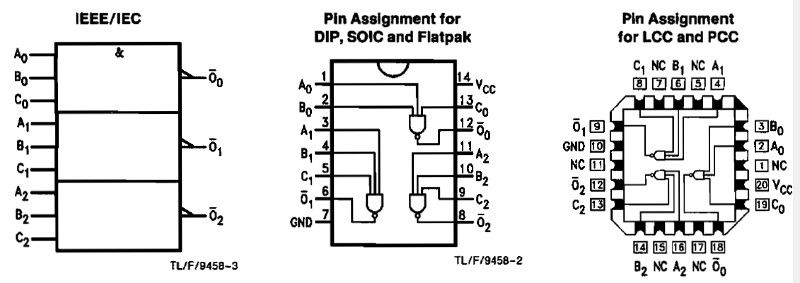
11 NAND (t.ex. 74LS11 eller 4011)
När någon av ingångarna är låg (L) så blir utgången hög (H).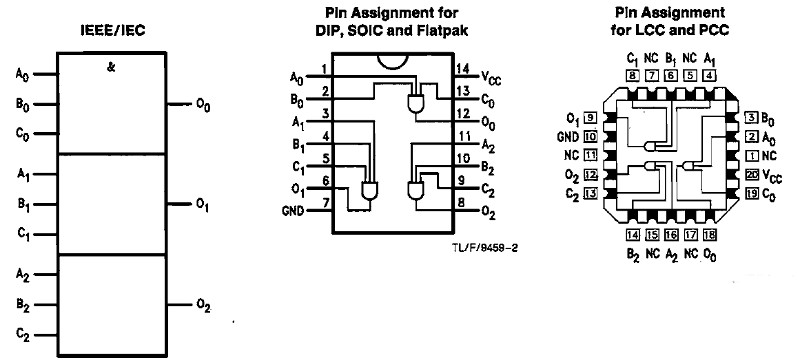
13 NAND (t.ex. 74LS13 eller 4013)
När någon av ingångarna är låg (L) så blir utgången hög (H).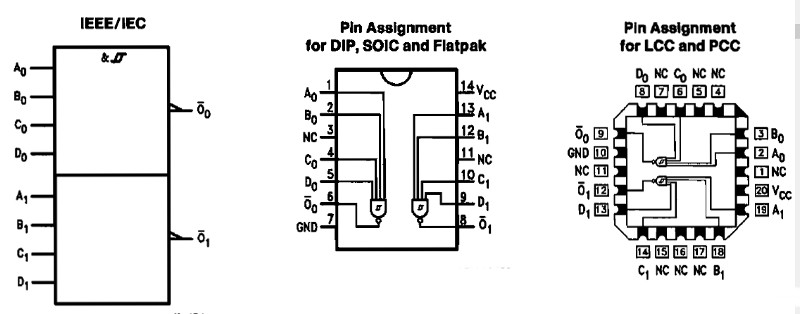
14 Hex Inverter (t.ex. 74LS14)
När en ingång är hög blir utgången låg och tvärtom.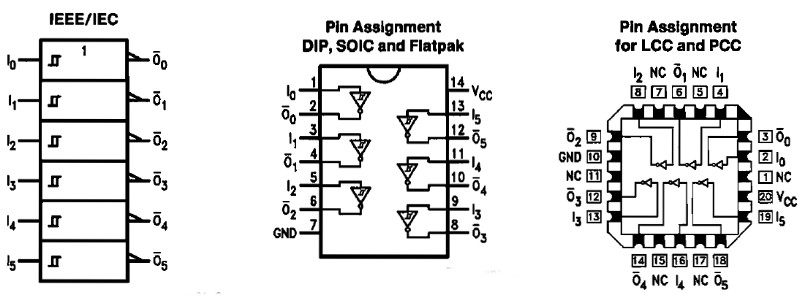
20 NAND (t.ex. 74LS20 eller 4020)
När någon av ingångarna är låg (L) så blir utgången hög (H).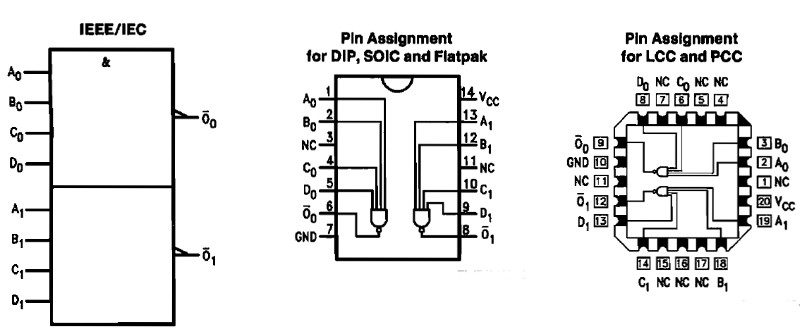
27 NOR (t.ex. 74LS27 eller 4027)
När någon av ingångarna är hög (H) så blir utgången låg (L).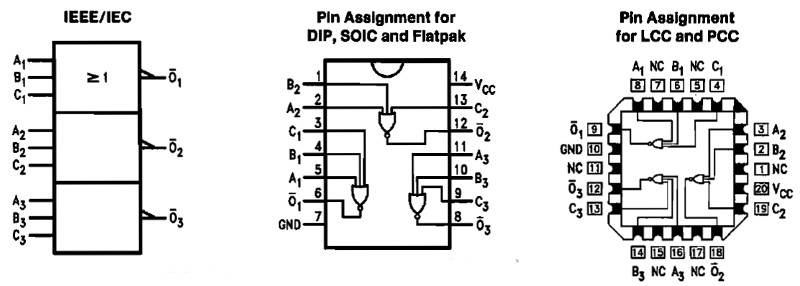
30 NAND (t.ex. 74LS30 eller 4030)
När någon av ingångarna är låg (L) så blir utgången hög (H).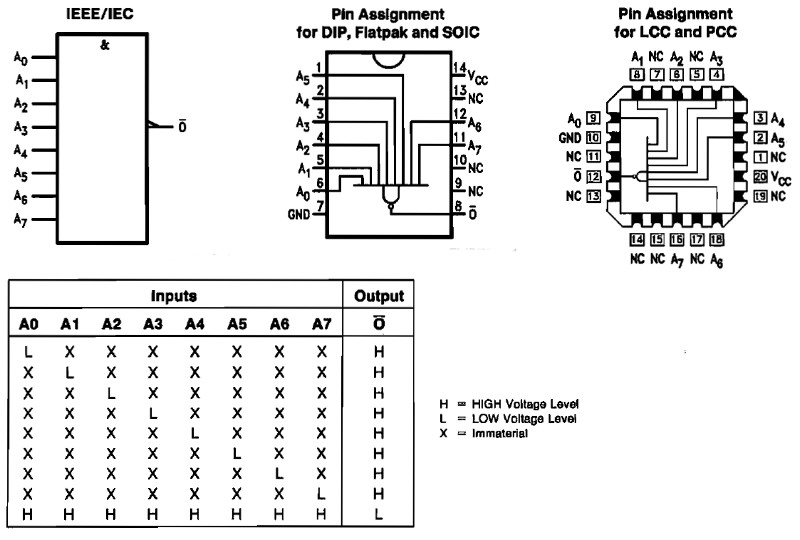
32 OR (t.ex. 74LS32)
Om någon av ingångarna är hög (H) så blir utgången hög (H).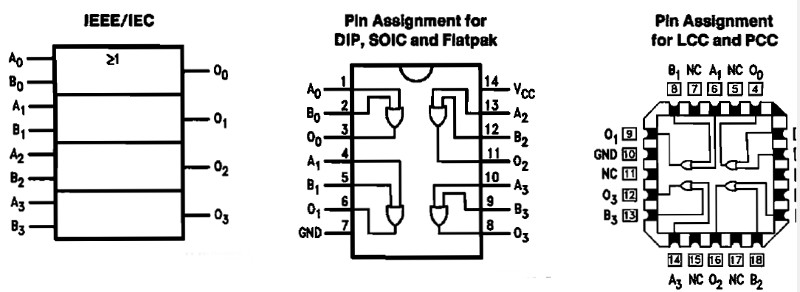
37 NAND (t.ex. 74LS37)
När någon av ingångarna är låg (L) så blir utgången hög (H).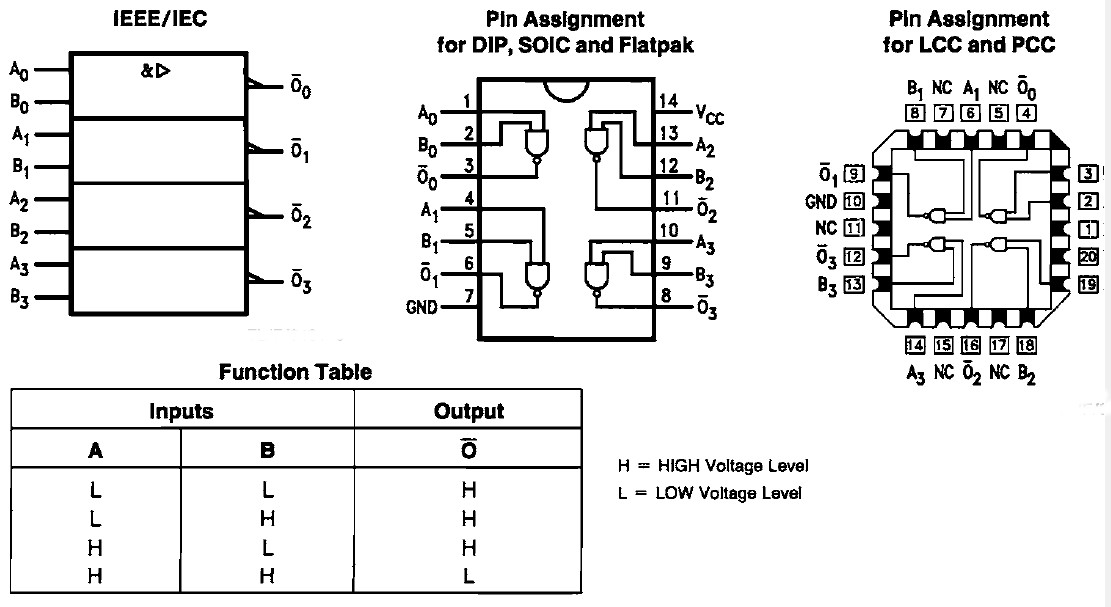
38 NAND (t.ex. 74LS38)
När någon av ingångarna är låg (L) så blir utgången hög (H).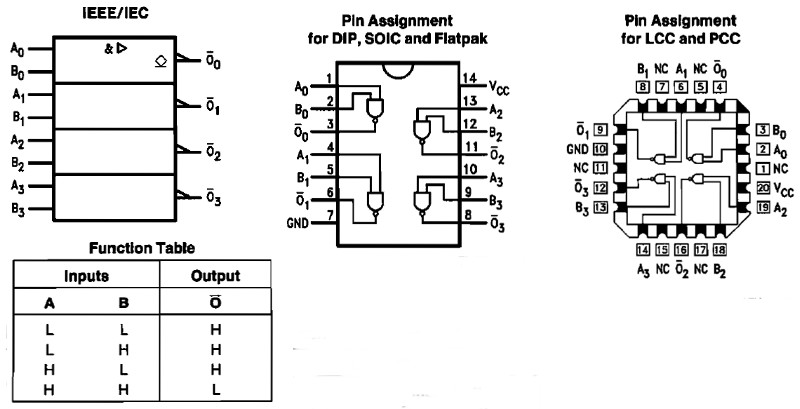
40 NAND (t.ex. 74LS40 eller 4040)
När någon av ingångarna är låg (L) så blir utgången hög (H).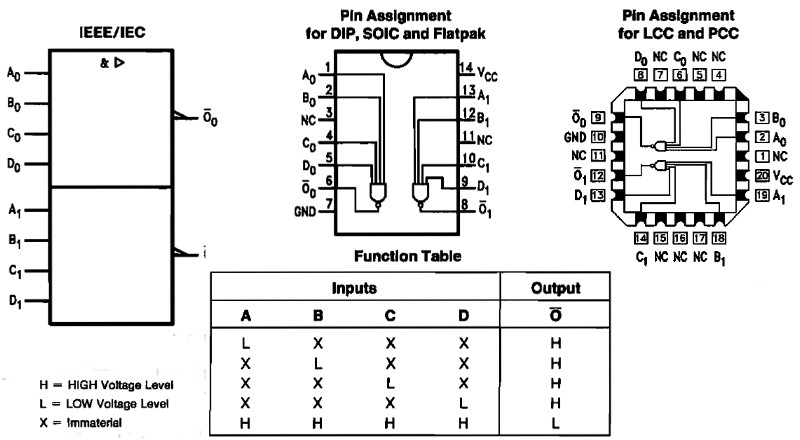
51 AND-OR-Invert (t.ex. 74LS51 eller 4051)
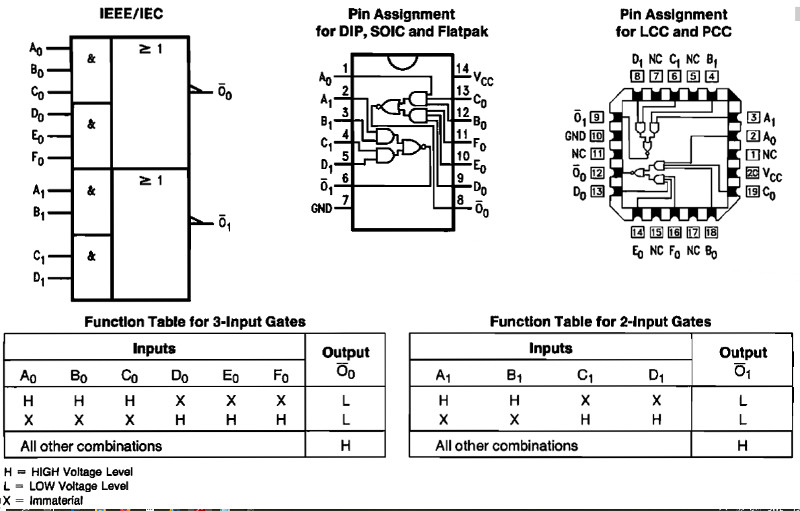
64 AND-OR-Invert (t.ex. 74LS64)
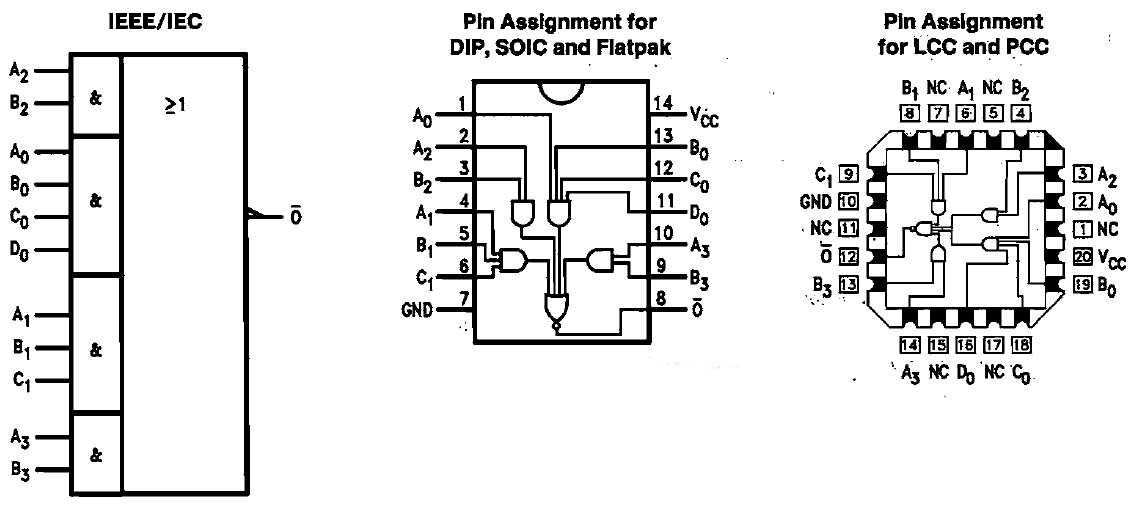
86 XOR (t.ex. 74LS86 eller 4086)
XOR är speciell på så vis att ugången blir hög (H) om en av 2 ingångar är hög (H). Om båda är låga (L) eller båda är höga (H), så blir utgången låg (L).