Sekventiell logik
Det som kännetecknar sekventiell logik är att någon utsignal i nätet återkopplas in i nätet igen som insignal och vi åstadkommer på detta vis ett minne i nätet. Detta minne blir en del av insignalerna i nätet och vi kan på så vis skapa ett beteende där vi får en sekvens av signaler som delvis beror på vad vi haft för signaler tidigare.
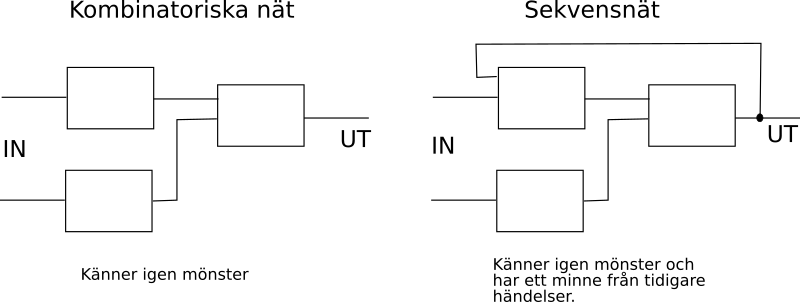
Detta skiljer sig alltså helt från kombinatoriska nät där en viss kombination av insignaler alltid ger samma utsignal.
Aktiv hög eller aktiv låg
Ett viktigt begrepp att förstå är vad som menas när man säger att en signal är aktiv. Med aktiv menar man det tillstånd när signalen bär det budskap den är tänkt göra. Det vanliga är att en signal är aktiv hög, att den "gör jobbet" (nollställer, sätter, skiftar eller vad kretsen nu ska göra) när signalen är hög. En Reset-signal som är aktiv hög, det innebär alltså att när Reset-signalen sätts till "1" eller "hög" då nollställs kretsen ifråga. Ibland är nämligen en ingång byggd så att den är aktiv låg. Det betyder - tvärtom - att signalen "gör jobbet" (nollställer, sätter, skiftar eller vad kretsen nu ska göra) när signalen är låg. Om en Reset -signal till en krets är aktiv låg, då innebär det att när signalen är "0" eller låg - så nollställs kretsen. När samma signal är "1" eller hög då händer ingenting, det är först när signalen är låg som saker händer.I nedan exempel på en krets finns 2 signaler SD ("set data") respektive CD ("clear data"). När SD blir låg så sätts utgången Q = 1 eller om CD blir låg så sätts utgången Q = 0.
SR-vippa
SR-vippans namn kommer av orden Set och Reset och det är också så funktionen enklast memoreras. Vi har en utsignal Q (eller den inverterade varianten av Q om det passar bättre) och 2 ingångar Set och Reset som är aktiva när de är låga.Vi har alltså följande sanningstabell med en SR-vippa byggd med NAND -grindar. Observera att tillståndet där både Set och Reset är aktiva samtidigt inte är tillåtet.
SR-vippa
| Set | Reset | Q |
| 1 | 1 | Q |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 0 | ej ok |
Skickar vi in en puls (L = Låg) på Reset -ingången så blir Q = Låg och förblir låg.
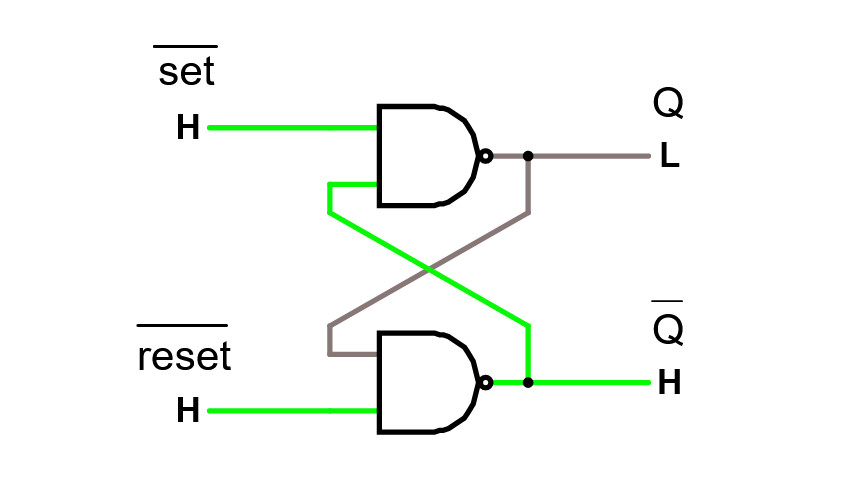
Skickar vi in en puls (L = Låg) på Set så blir Q = Hög och förblir i detta tillstånd.
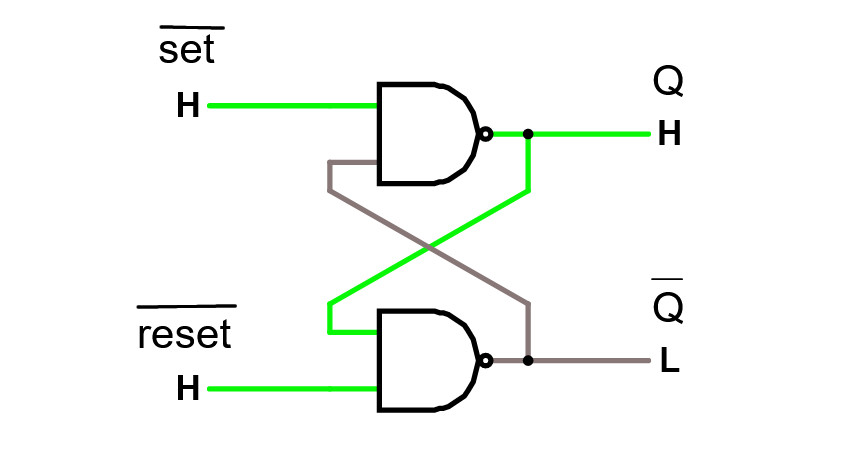
Studera SR -vippan i simulatorn.
Om vi skickar in en puls på Reset -ingången som är L = Låg med jämna mellanrum så får vi en självnollställande SR -vippa. Om vi skickar in L = Låg på Set så kommer utgången Q blir Hög en kortare eller längre stund, för att sedan nollställas automatiskt.
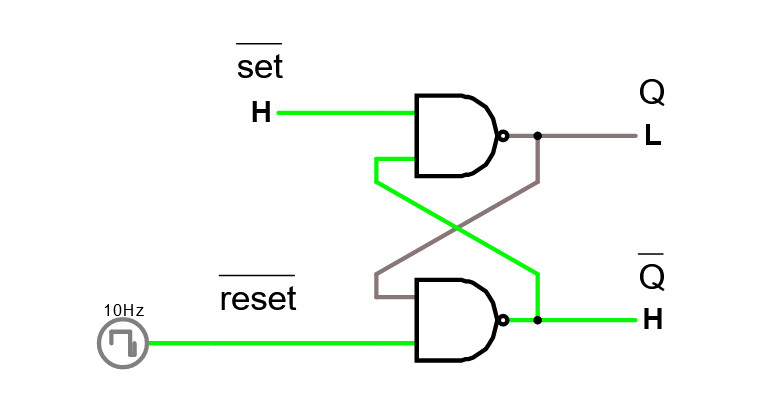
Studera den självnollställande SR -vippan i simulatorn.
Ett användningsområde för SR -vippan är för att få bort kontaktstuds.
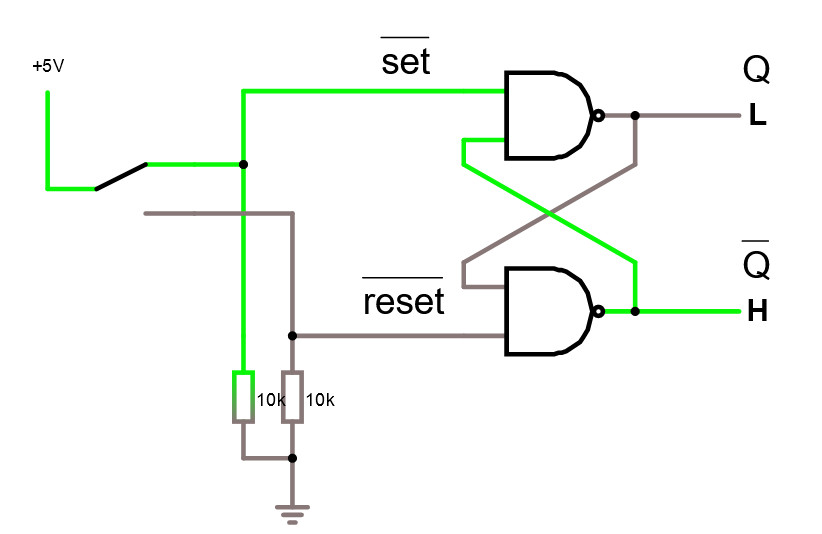
Ta bort kontaktstuds med en SR-vippa i simulatorn.
En SR -vippa byggd med transistorer nedan.
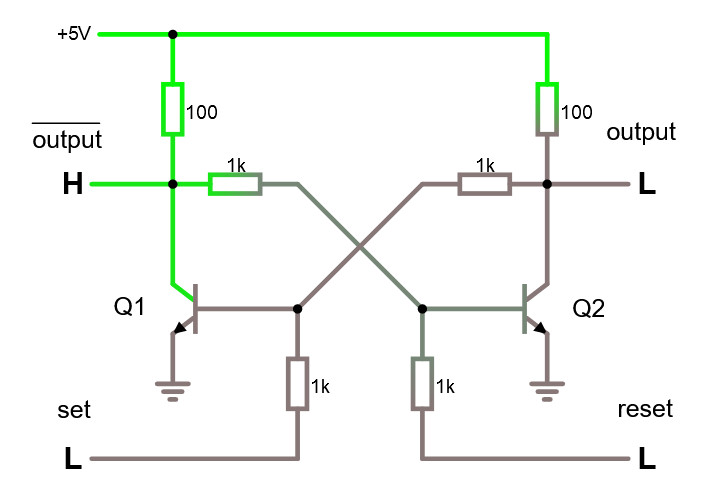
Studera transistor-SR-vippan i simulatorn.
Klockad SR-latch
En klockad SR -latch innebär att vi lagt till lite logik för att enbart släppa igenom förändringar, när klocksignalen är hög. Denna klocklogik vänder också på insignalerna, så nu är Set aktiv som hög och Reset aktiv som hög. Vi har alltså följande sanningstabell.Klockad SR-vippa
| Clk | Set | Reset | Q |
| 0 | X | X | Q |
| 1 | 0 | 0 | Q |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | ej ok |
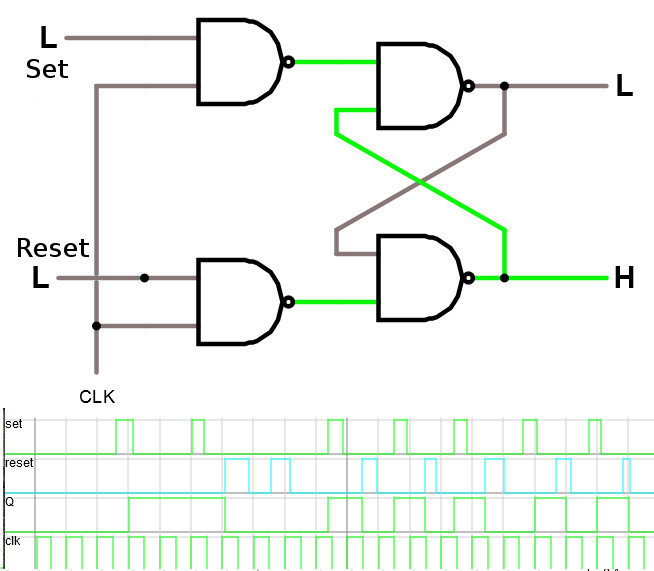
Studera den klockade SR-latchen i simulatorn.
D-latch
D-latchen är en klockad SR-vippa fast med skillnaden att vi ersatt Set och Reset med en enda signal som vi kallar D (D = Data). Så D-latchen fungerar som så att den låter utgången följa ingången (Q = D) när klocksignalen är hög.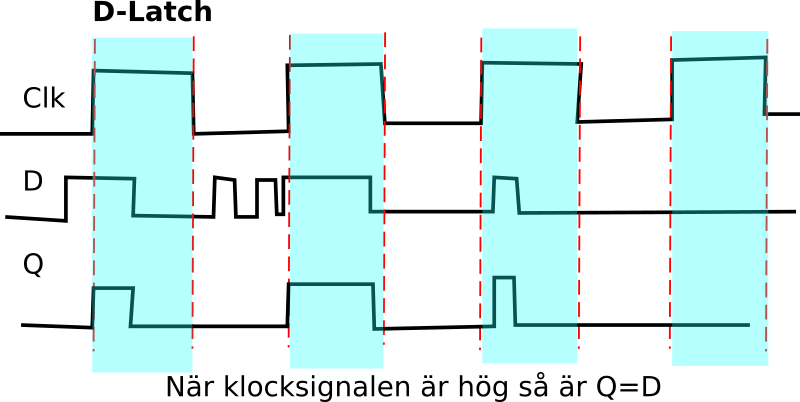
D-latch
| Clk | D | Q |
| 0 | X | Q |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Den lilla skillnaden mellan en klockad SR -latch och D-latchen är alltså att Reset försvunnit och istället ersatts med den inverterade Set -signalen, vilket trollar bort det otillåtna tillståndet på SR -latchen.
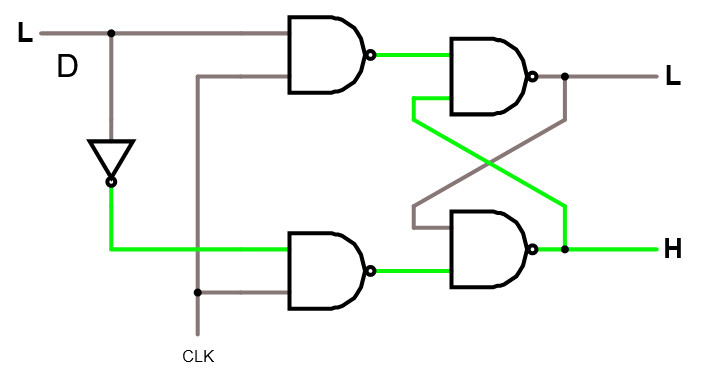
Studera D-latchen i simulatorn.
D-FlipFlop
D-FlipFlop fungerar nästan som D-latchen fast med skillnaden att Q sätts till värdet av D när klocksignalen stiger (stigande flank).D-flipflop
| Clk | D | Q |
| ↑1 | 0 | 0 |
| ↑1 | 1 | 1 |
| X | X | Q |
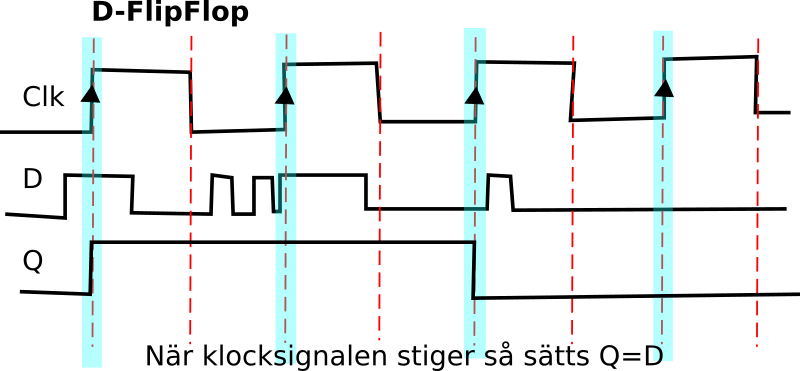
Logiken nedan för D-flipflop blir alltså lite mer komplicerad.
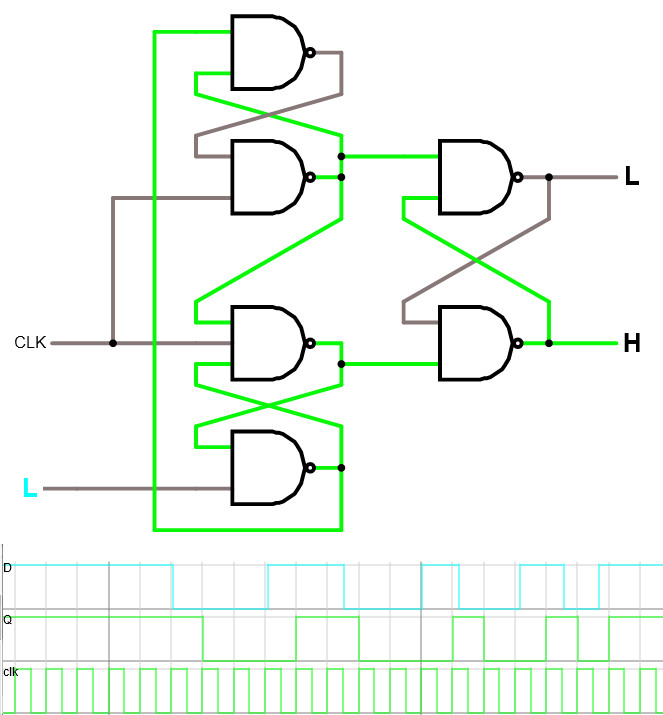
Klicka här för att titta på D-flipflop i simulatorn.
En D-flipflop har följande symbol.
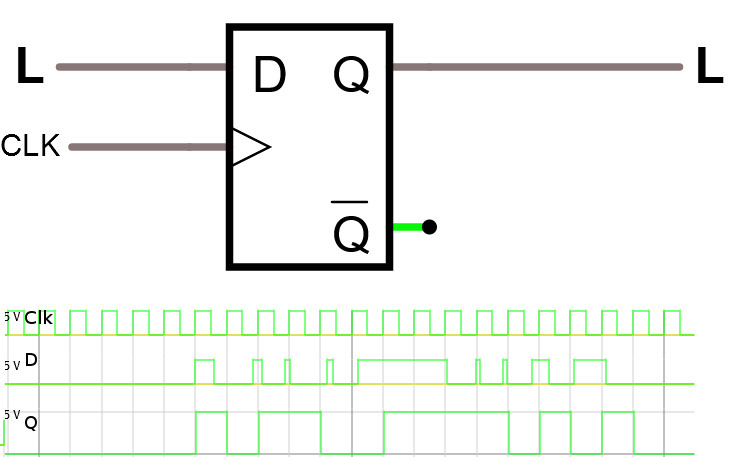
Titta på D-flipflop i simulatorn.
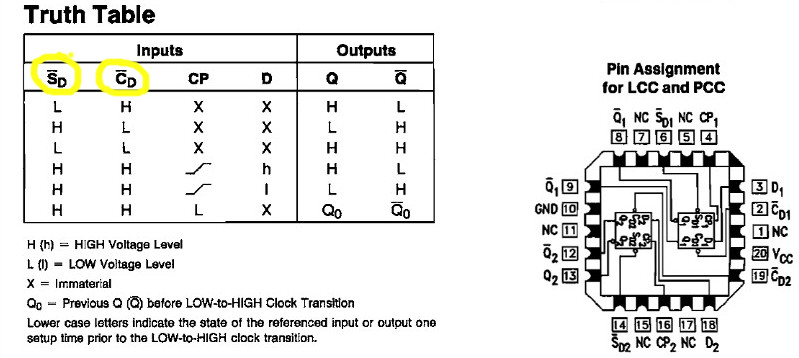
Ett vanligt tillägg, inspirerat från SR -vippan, t.ex. 74LS74, är extra ingångar för Set och Reset. Det brukar ha beteckningarna SD och CD. Dvs Set och Clear och de brukar vara aktiva låga. Sanningstabellen kan då se ut såhär.
D-flipflop 74LS74
| SD | CD | Clk | D | Q | Q |
| L | H | X | X | 1 | 0 |
| H | L | X | X | 0 | 1 |
| L | L | X | X | 1 | 1 |
| H | H | ↑1 | 0 | 0 | 1 |
| H | H | ↑1 | 1 | 1 | 0 |
| H | H | L | X | Q | Q |
Dvs, sålänge SD och CD är höga (observera att de är aktiva som låga) fungerar D-flipflop som normalt. Men om SD är aktiv så blir Q = 1 och om CD är aktiv så clear:as utgången (blir noll). Om både SD och CD är aktiva (låga) så är både Q och Q höga samtidigt.
JK-vippa
J och K i namnet JK-vippa kommer inte från något speciellt, mer än att de är konsekutiva i alfabetet. Hos JK -vippan har det tidigare otillåtna tillståndet där båda ingångarna är höga fått en mening - nämligen att tillståndet Q inverteras.Det förekommer både inverterade och icke inverterade clock -ingångar, vilket betyder att vissa JK-vippor triggar på negativ flank och andra på positiv.
JK-vippa
| Clk | J | K | Q |
| ↓0 | 0 | 0 | Q |
| ↓0 | 0 | 1 | 0 |
| ↓0 | 1 | 0 | 1 |
| ↓0 | 1 | 1 | Q |
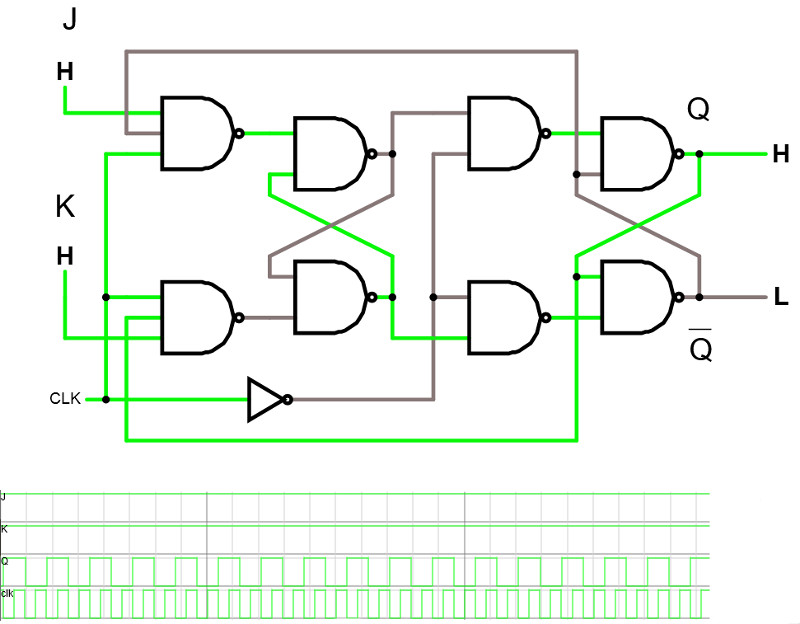
Titta på JK-flipflop'en i simulatorn.
JK-vippan har följande symbol.
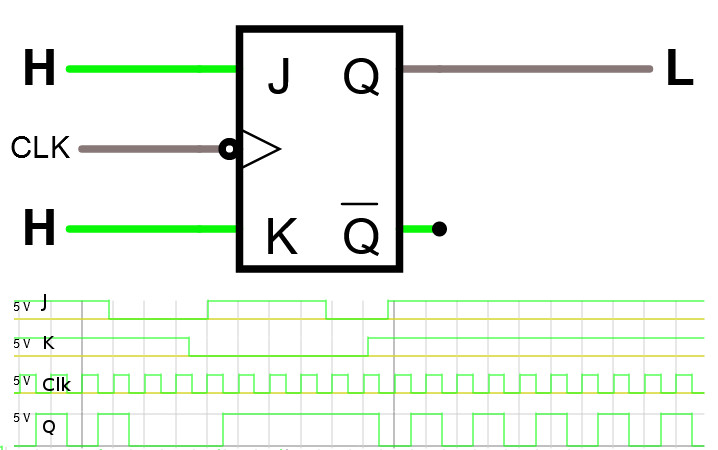
Studera JK-vippan i simulatorn.
Ett viktigt användningsområde för denna toggle -finess hos JK -vippan är att vi kan bygga upp räknare med hjälp av JK -vippor.
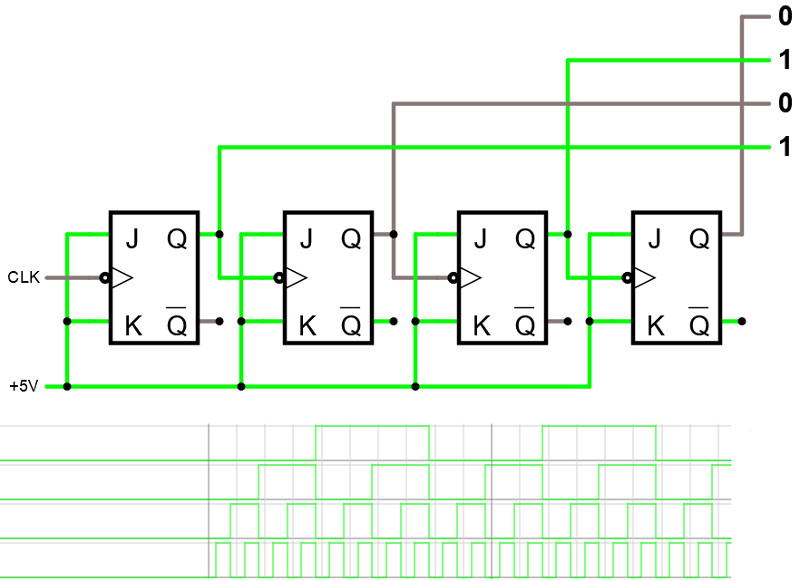
Studera räknaren i simulatorn.
Det finns många olika typer av JK -vippor. Ett vanligt tillägg, inspirerat från SR -vippan, är extra ingångar för Set och Reset. Det brukar ha beteckningarna SD och CD. Dvs Set och Clear och de brukar vara aktiva låga.
74 Dual D-type Flip Flop (t.ex. 74LS74)
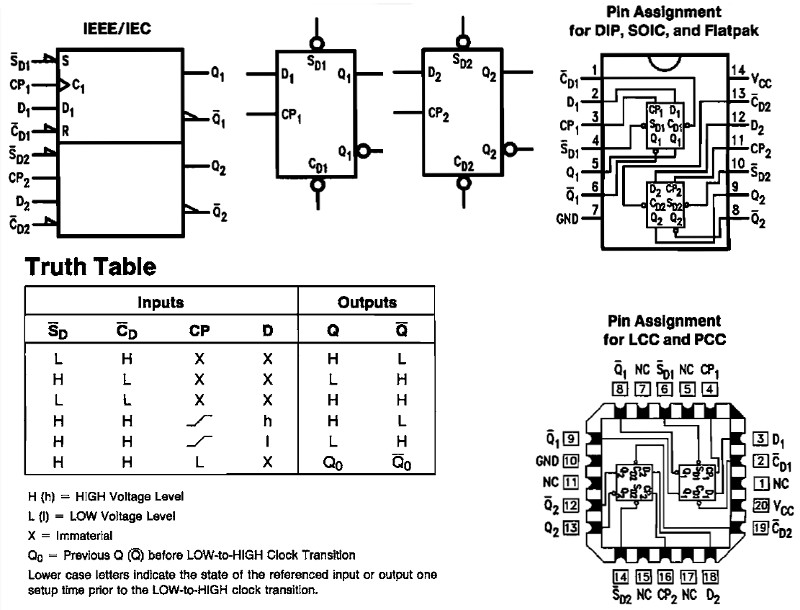
109 JK Flip Flop (t.ex. 74LS109 eller 40109)
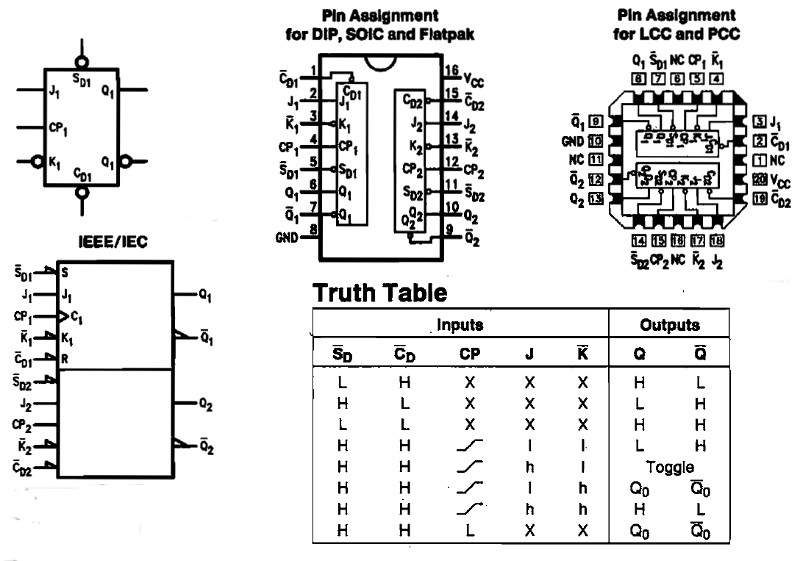
112 JK Flip Flop (t.ex. 74LS112)
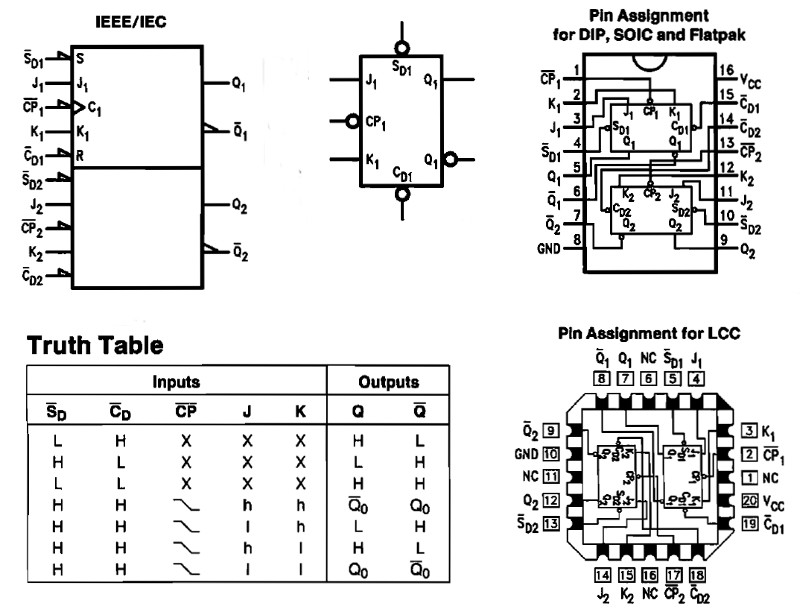
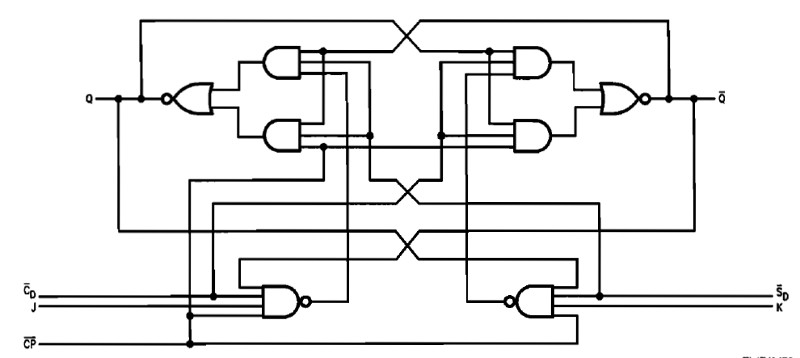
Diagram JK Flip Flop
Annons
Egen domän, epost & webbsida
Från 120 + 140 = 260 kr per år + moms för Brons -konto med .com -domän.
Bästa sättet att lära sig något, är att 1) ha något att Meka med 2) Meka.
Detsamma gäller förstås internet och webbsidor. Vill du lära dig göra roliga saker, t.ex. en fixa en egen hemsida på en egen domän eller installera en hemma-server på egen domän? Skaffa ett konto på ett billigt hjälpsamt webbhotell, där du kan ställa många dumma frågor till supporten. Välkommen!
Detsamma gäller förstås internet och webbsidor. Vill du lära dig göra roliga saker, t.ex. en fixa en egen hemsida på en egen domän eller installera en hemma-server på egen domän? Skaffa ett konto på ett billigt hjälpsamt webbhotell, där du kan ställa många dumma frågor till supporten. Välkommen!
Kontrollpanel (Direct Admin), där du kan lägga till epostadresser, installera wordpress för en företagssida eller privat blogg, lägga till subdomäner, tanka upp filer, ändra DNS -pekare och massor med annat. Behöver du hjälp fixa webbsida? Vi hjälper dig. Börjar ditt nuvarande webbhotell bli störande dyrt? Hör av dig, vi kan troligtvis hjälpa dig med flytten.
Karla Hosting AB • https://karlahosting.se